数据结构-树(数据结构树的度是什么)

南窗分类：IT技术人气：118 回帖：0 发布于1年前收藏

树

树的特点

每个结点有零个或多个子节点
没有父节点的结点为根结点
每个非根结点只有一个父节点
每个结点及其后代结点整体上可以看作是一棵树，称为当前结点的父结点的一个子树

树的相关术语

结点的度：

一个结点含有的子树的个数称为该结点的度

叶节点：

度为0的结点称为叶结点，也可以叫做终端结点。

分支结点：

度不为0的结点称为分支结点，也可以叫做非终端结点

结点的层次：

从根结点开始，根结点的层次为1，根的直接后继层次为2，一次类推

结点的层序编号：

将树中的结点，按照从上层到下层，同层从左到右的次序排成一个线性序列，把他们编成连续的自然数

树的度：

树中所有结点的度的最大值

树的高度

树中结点的最大层次

森林：

m(m>=0)个互不相交的树的集合，将一颗非空树的根结点删去，树就变成一个森林，给森林增加一个统一的根节点，森林就变成了一棵树

孩子结点：

一个结点的直接后继结点称为该结点的孩子结点

双亲结点（父结点）：

一个结点的直接前驱称为该结点的双亲结点

兄弟结点：

同一双亲结点的孩子节点间互称兄弟结点

二叉树

基本定义

二叉树就是度不超过2的树（每个结点最多有两个子结点）

满二叉树：一个二叉树，如果每一个层的结点树都达到最大值，就称这个二叉树是满二叉树。

完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。

二叉查找树设计

类名	Node
构造方法	Node(Key key,Value value,Node left,Node right);创建Node对象
成员变量	1. public Node left:记录左子结点2.public Node right:记录右子结点3.public Key key:存储键4.public Value value:存储值

类名	BinaryTree,Value value>
构造方法	BinaryTree():创建BinaryTree对象
成员变量	1. private Node root:记录根节点2.private int N:记录树中元素的个数
成员方法	1.public void put(Key key,Value value):向树中插入一个键值对2.private Node put(Node x,Key key,Value val):给指定树x上，添加键一个键值，并返回添加后的新树3.public Value get(Key key):根据key，从书中找出对应的值4.private Value get(Node x,Key key):从指定的树x中，找出key对应的值5.public void delete(Key key):根据key，删除树中对应的键值对6.private Node delete(Node x,Key key):删除指定树x上的键为key的键值对，并返回删除后的新树7.public int size():获取树中元素的个数

代码实现

public class BinaryTree,Value> {
    //记录根结点
    private Node root;
    //记录树中元素的个数
    private int N;
    private class Node{
        //储存键
        public Key key;
        //储存值
        private Value value;
        //记录左节点
        public Node left;
        //记录右节点
        public Node right;
        public Node(Key key,Value value,Node left,Node right){
            this.key=key;
            this.value=value;
            this.left=left;
            this.right=right;
        }
    }

    /**
     * 返回树的长度
     * @return
     */
    public int size(){
        return N;
    }

    /**
     * 向树中添加元素key-value
     * @param key
     * @param value
     */
    public void put(Key key , Value value){
        root = put(root,key,value);
    }

    /**
     * 向指定的树中添加key-value,并返回添加元素后新的树
     * @param x
     * @param key
     * @param value
     * @return
     */
    private Node put(Node x,Key key,Value value){
         //如果x子树为空
        if(x==null){
            N++;
            return new Node(key,value,null,null);
        }
        //如果x子树不为空

        //比较x结点的健和key的大小

        int cmp = key.compareTo(x.key);
        if(cmp>0){
            //如果key大于x结点的健，则继续找x结点的右子树
            x.right = put(x.right,key,value);
        }else if (cmp<0){
            //如果key小于x结点的键，则继续找x结点的左子树
            x.left = put(x.left,key,value);
        }else {
            //如果key等于x结点的键，则继续找x结点的左子树
            x.value = value;
        }
        return x;
    }

    //查找树中指定key对应的value
    public Value get(Key key){
        return get(root,key);
    }

    //从指定的树x中查找key对应的值域
    public Value get(Node x,Key key){
        //x树为null
        if(x==null){
            return null;
        }
        //x树不为null
        //比较key和x结点的键的大小
        int cmp = key.compareTo(x.key);
        if(cmp>0){
            //如果key大于x结点的健，则继续找x结点的右子树
            return get(x.right,key);
        }else if (cmp<0){
            //如果key小于x结点的键，则继续找x结点的左子树
            return get(x.left,key);
        }else {
            //如果key等于x结点的键，就找到了键为key的结点，只需要返回x结点的值即可
            return x.value;
        }
    }

    //删除树中key对应的value
    public void delete(Key key){
        delete(root,key);
    }

    //删除指定树x中的key的value，返回删除后的树
    public Node delete(Node x , Key key){
        //x树为null
        if(x==null){
            return null;
        }
        //x树不为null
        int cmp = key.compareTo(x.key);
        if(cmp>0){
            //如果key大于x结点的健，则继续找x结点的右子树
            x.right = delete(x.right,key);
        }else if (cmp<0){
            //如果key小于x结点的键，则继续找x结点的左子树
            x.left = delete(x.left,key);
        }else {
            //让元素个数减一
            N--;
            //如果key等于x结点的键，完成真正的删除结点动作，要删除的结点就是x

            //首先得找到右子树中最小的结点
            if(x.right==null){
                return x.left;
            }

            if(x.left==null){
                return x.right;
            }
            Node minNode = x.right;
            while(minNode!=null){
                minNode = minNode.left;
            }
            //删除右子树中最小的结点
            Node n = x.right;
            while (n.left!=null){
                if(n.left.left==null){
                    n.left=null;
                }else{
                    //变换n结点即可
                    n=n.left;
                }
            }

            //让x结点的左子树，成为minNode的左子树
            minNode.left=x.left;
            //让x结点的右子树，成为minNode的右子树
            minNode.right=x.right;
            //让x结点的父结点指向minNode
            x = minNode;
        }
        return null;
    }
}

查找二叉树最小的键

方法设计

public Key min()	找出树中最小的键
private Node min(Node x)	找出指定树x中，最小健所在的结点

    //找出整个树中最小的健
    public Key min(){
        return min(root).key;
    }
    //找出指定x中最小的键所在的结点
    private Node min(Node x){
        if(x.left!=null){
            return  min(x.left);
        }else{
            return x;
        }
    }

查找二叉树最大的键

方法设计

public Key max()	找出树中最大的键
private Node max(Node x)	找出指定树x中，最大健所在的结点

    //找出整个树中最大的健
    public Key max(){
        return max(root).key;
    }
    //找出指定x中最小的键所在的结点
    private Node max(Node x){
        if(x.right!=null){
            return max(x.right);
        }else{
            return x;
        }
    }

二叉树的基础遍历

分为三种遍历方式

前序遍历

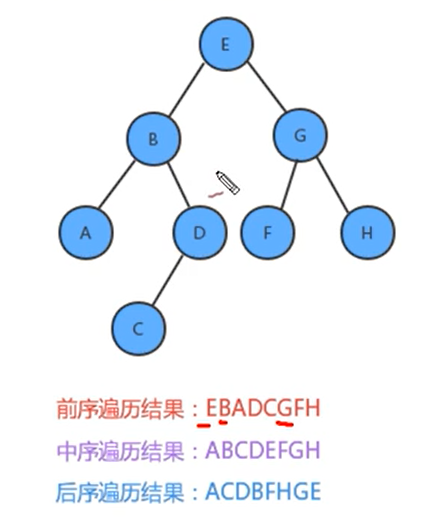
先访问根节点，然后再访问左子树，最后访问右子树

中序遍历

先访问左子树，中间访问根节点，最后访问右子树

后序遍历

先访问左子树，在访问右子树，最后访问根节点

前序遍历

public Queue preErgodic():使用前序遍历，获取整个树中的所有键

private void preErgodic(Node x,Queue keys)使用前序遍历，把指定树x中所有健放入到key队列中

    //获取整个树中所有的键
    public Queue preErgodic(){
        Queue keys = new Queue<>();
        preErgodic(root,keys);
        return keys;
    }

    //获取指定树x的所有键，并放到keys队列中
    private  void preErgodic(Node x,Queue keys){
        if(x==null){
            return;
        }
        //把x结点的key放入到keys中
        keys.enqueue(x.key);
        //递归遍历x结点的左子树
        if(x.left!=null){
            preErgodic(x.left,keys);
        }
        //递归遍历x结点的右子树
        if(x.right!=null){
            preErgodic(x.right,keys);
        }
    }

中序遍历

public Queue midErgodic()使用中序遍历，获得整个树中的所有键

private void midErgodic(Node x,Queue keys)使用中序遍历，把指定树x中的所有键放入到keys队列中

实现：

找到当前结点的左子树，如果不为空，递归遍历左子树
把当前结点的key放入到队列中
找到当前结点的右子树，如果不为空，递归遍历右子树

//使用中序遍历，获取指定树x中所有的键，并存放到key中
    private void midErgodic(Node x,Queue keys){
        //先递归，把左子树中的键放到keys中
        if(x==null){
            return;
        }
        //先递归，把当前结点x的键放到keys中
        if(x.left!=null){
            midErgodic(x.left,keys);
        }
        //把当前结点x的键放到keys中
        keys.enqueue(x.key);
        //再递归，把右子树中的键放到keys中
        if(x.right!=null){
            midErgodic(x.right,keys);
        }
    }

后序遍历

public Queue afterErgodic()使用后序遍历，获取整个树中的所有键

private void afterErgodic(Node x,Queue keys)使用后序遍历，把指定树x中的所有键放入到keys队列中

实现

找到当前结点的左子树，若不为空，递归遍历左子树
找到当前结点的右子树，如果不为空，递归遍历右子树
把当前结点的key放入到队列中

//使用后序遍历把指定树x中所有的键放入到keys中
    private void afterErgodic(Node x,Queue keys){
        if(x==null){
            return;
        }
        //把左子树所有的键放入到keys中
        if(x.left!=null){
            afterErgodic(x.left,keys);
        }
        //通过递归把右子树中所有的键放入到keys中
        if(x.right!=null){
            afterErgodic(x.right,keys)
        }
        //把x结点的键放入到keys中
        keys.enqueue(x.key);
    }

层序遍历

从根节点（第一层）开始，依次向下，获取每一层所有结点的值，

public Queue layerErgodic()使用层序遍历，获取整个树中所有的键

实现

创建队列，存储每一层的结点
使用循环队列中弹出的一个结点

获取当前结点的key
如果当前结点的左子节点不为空，则把左子节点放入到队列中
如果当前结点的右子节点不为空，则把右子节点放入到队列中

//层序遍历
    public Queue layerErgodic() throws InterruptedException {
        //定义两个队列，分别存储树中的键和树中的结点
        Queue keys = new Queue<>();
        Queue nodes = new Queue<>();
        //默认往队列中放入根节点
        nodes.enqueue(root);
        while(nodes.isEmpty()){
            //从队列中弹出结点，把key放入到keys中
            Node n = nodes.dequeue();
            keys.enqueue(n.key);
            //如果当前结点的左子节点不为空，则把左子节点放入到队列中
            if(n.left!=null){
                nodes.enqueue(n.left);
            }
            //如果当前结点的右子节点不为空，则把右子节点放入到队列中
            if(n.right!=null){
                nodes.enqueue(n.right);
            }
        }
        return keys;
    }

二叉树的最大深度问题

实现

public int maxDepth计算整个树的最大深度

private int maxDepth(Node x) 计算指定树x的最大深度

步骤：

如果根节点为空，则最大深度为0；
计算左子树的最大深度；
计算右子树的最大深度；
当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1

//获取整个树的最大深度
    public int maxDepth(){
        return maxDepth(root);
    }

    //获取指定树x的最大深度
    private int maxDepth(Node x){
        if(x==null){
            return 0;
        }
        //x的最大深度
        int max=0;
        //左子树的最大深度
        int maxL=0;
        //右子树的最大深度
        int maxR=0;
        //计算x结点左子树的最大深度
        if(x.left!=null){
            maxL = maxDepth(x.left);
        }
        //计算x结点右子树的最大深度
        if(x.right!=null){
            maxR = maxDepth(x.right);
        }
        //比较左子树最大深度和右子树最大深度，取较大值+1即可
        max = maxL>maxR?maxL+1:maxR+1;
        return max;
    }

版权属于：吃猫的鱼

本文链接： https://www.fish9.cn/archives/395/

作品声明：未经许可，禁止转载！

标签：数据结构,key,private,public,queue,

树