在音频领域,mel频谱和mfcc是非常重要的特征数据,在深度学习领域通常用此特征数据作为网络的输入训练模型,来解决音频领域的各种分类、分离等业务,如端点侦测、节奏识别、和弦识别、音高追踪、乐器分类、音源分离、回声消除等相关业务。
当然,针对深度学习音频领域的业务,不是用下这两个特征、选几个网络、打个标签,放数据训练就完事了, 仅仅基于mel频谱和mfcc这两个特征,解决好上述业务某些情况下还是远远不够的,熟悉这些特征的内在逻辑性、衍生细节和延展,才能更好的结合深度学习解决业务问题。
下面讲解mel频谱和mfcc特征的算法流程和一些细节、延展,这些细节从局部角度来看,都会影响到最终特征呈现的细节差异,这些差异放大到模型训练结果的准确性、鲁棒性上怎么样是非常值得研究的,某些情况下可能会有质的变化,质的变化无论正向还是负向都是值得关注的,最怕的是没变化;同时,一些问题的延展从广义角度来看,带来不同的特征组合、网络结构设计思考等也是解决业务问题非常重要的思想源泉。
设 sr 为采样率,fftLength 为帧长度,slideLength 为滑动长度
下面是一张mel频谱和mfcc的大概算法流程图。
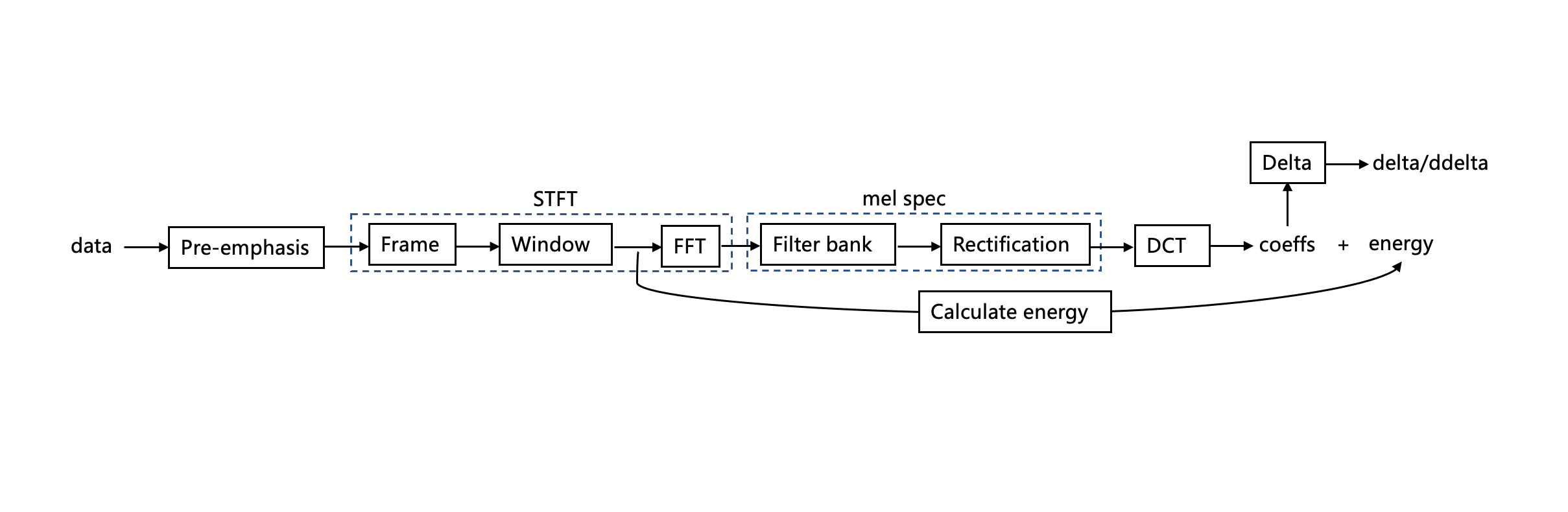
如流程图所示的第1步,属于信号的预处理,补偿高频分量损失,提升高频分量,一般情况下可以忽略此步骤,属于信号的简单增强,对特征有一定的提升效果。公式如下
x[n]=x[n]-\alpha x[n-1]\alpha 一般取0.97 公式属于差分一阶即高通滤波器。
现实中大多数信号都是非平稳的,但大多数短时间内可以近似看做是平稳的,可以用短时傅里叶变换表现非平稳信号频域特征。 一般语音中采用10ms~30ms左右,乐音中可以更长一些64ms~256ms。
分帧涉及到前后重叠(overlap),一般情况下以滑动帧长的1/4或1/2(前后重叠3/4或1/2)进行,即 slideLength=\cfrac{fftLength}4或\cfrac{fftLength}2 。
加窗目的是减少频谱泄露,降低泄漏频率干扰,提升频谱效果,默认不处理即加矩形窗(Rect),干扰泄漏较严重,一般情况下加Hann窗,针对大多数信号都有不错的效果。公式如下
w(n)=0.5\left( 1-\cos \left(2\pi \cfrac n{N} \right)\right) , 0 \le n \le NHann为余弦窗,N表示阶数。
分帧加窗傅里叶变换即短时傅里叶变换。公示如下
X(\tau,f)=\int_{-\infty}^\infty x(t)w(t-\tau)e^{-j2\pi f t}dt X(m,k)=\sum_{n=0}^{N-1} x[n]W[n-m]e^{\frac{-j2\pi kn}{N} }设数据长度为 dataLength, t=\begin{cases} \cfrac{(dataLength-fftLength)}{slideLength}+1, &无填充 \\ \cfrac{dataLength}{slideLength}+1 , &填充fftLength\end{cases}
STFT属于标准的数学变换,为复数域,尺寸为 t*fftLength ,为表示区分,一般的如|X(m,k)| 取模,尺寸为t*(fftLength/2+1) 表示为STFT频谱,有以下类型频谱。
|X(m,k)| ,STFT幅值频谱undefined|X(m,k)|^2 ,STFT功率频谱undefined\log(|X(m,k)|) ,STFT dB(分贝)频谱undefined20\log\left(\cfrac{|X(m,k)|}{fftLength}\right) ,STFT标准dB频谱
注:
dB频谱属于相对谱,加减乘除对频率相对dB值没影响,标准dB频谱相当于建立一个基准参考线,方便分析频谱和量化,大多数频谱示例都是此种类型。undefined深度学习中使用dB谱训练大多数要优于其它数值类型的频谱。
此过程是计算mel频谱关键部分和mfcc的重要一步。流程图如下

mel刻度(scale)是一种基于人耳听觉设计的log压缩刻度,人耳针对低频比较敏感,高频不太敏感,比如110hz和116hz一般人都能区分出来,但4000hz和4100hz大部分分不出来。mel刻度和hz的转换公式如下
\begin{cases} mel=2595\log_{10}(1+\cfrac{hz}{700}) \\ hz=700(10^{\frac{mel}{2595}}-1) \end{cases}图中前三个步骤即根据业务fre边界和num频带个数计算mel刻度下所映射的freBandArr。
接下来就是STFT频带如何映射到mel刻度的频带,用频带加三角窗进行计算mel刻度的filterBank matrix,三角窗公式如下
w(n)=\begin{cases} \cfrac{2n}N, & 0 \le n \le \cfrac N{2} \\ 2-\cfrac{2n}N, & \cfrac N{2} \le n \le N \end{cases}如下图
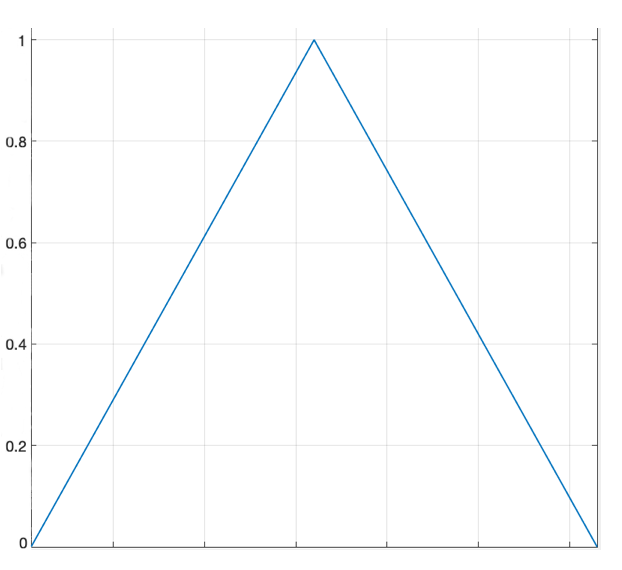
当然这个是对称的,线性频带用对称的没问题,mel刻度产生的频带log比例,左右不会对称,这时候使用三角窗就是非对称的,下面是mel刻度的filterBank matrix公式
w(k,h)=\begin{cases} \cfrac{h-f_{k-1}}{f_k-f_{k-1}}, & f_{k-1} \lt h\le f_k \\ \cfrac{f_{k+1}-h}{f_{k+1}-f_k} , & f_{k} \lt h\le f_{k+1} \\ 0, & other \end{cases}下面给出一个简单的示意图
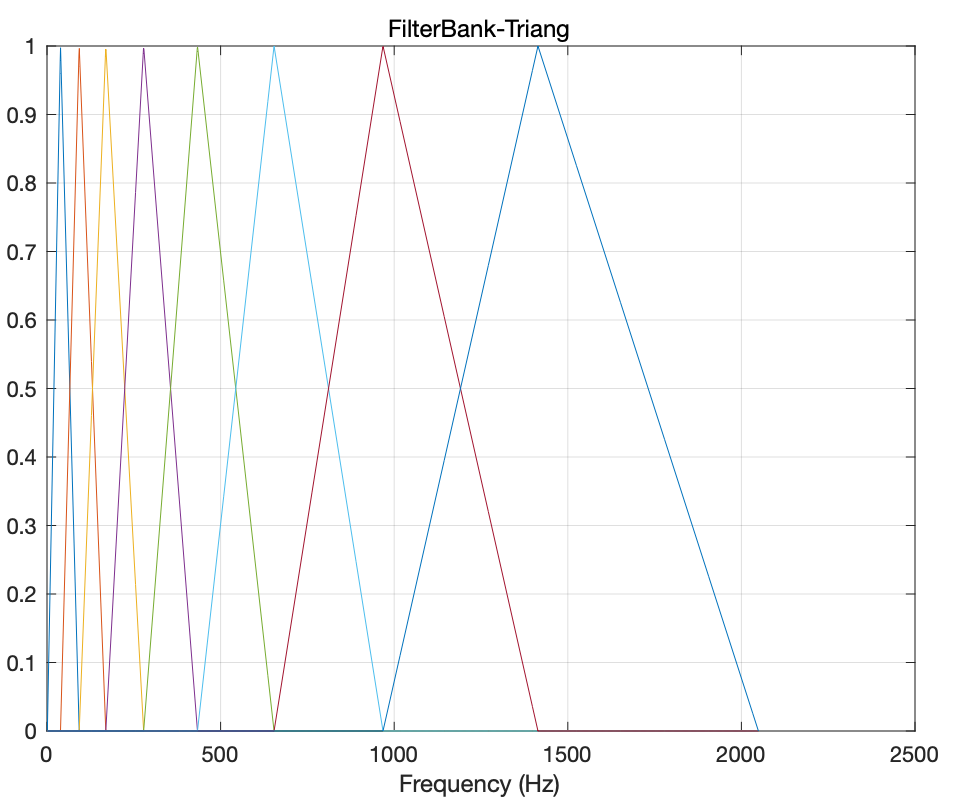
最后,一般使用STFT功率频谱和filterBank matrix做矩阵乘法运算即得出mel功率频谱。
对上一步mel功率频谱取log运算,即mel dB频谱就是通常所使用的“mel频谱”,一般情况下5、6步作为一个整体看待,合到一块可以理解为mel频谱的计算。
下面是STFT频谱和mel频谱(num=128)的效果对比图。
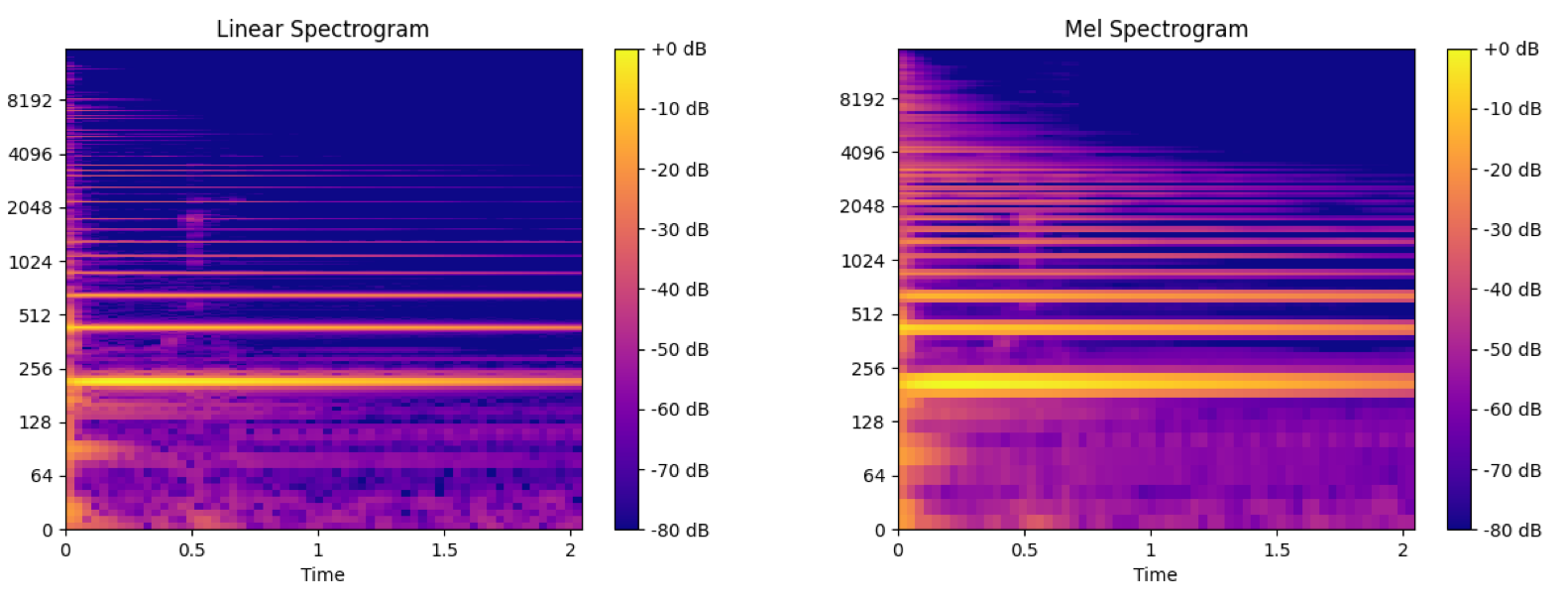
离散余弦变换,即数据为偶函数的实数傅里叶的变换,有去相关和能量集中特点。公式如下
X[k]=\sum_{n=0}^{N-1}x[n]e^{\frac{-j2\pi kn}{N} }=\sum_{n=0}^{N-1}x[n] \left[ \cos(\frac{2\pi kn}{N} )-j\sin( \frac{2\pi kn}{N} ) \right]当\sin(\theta)=0 ,即DCT变换, \cos(\theta)=0 ,即DST变换。
DCT变换,属于数据高度去相关后的特征反映,由于能量集中的特点,在数据压缩领域广泛常用,一般的,DCT考虑到数据解析延拓时中间点选取、边界、方式等情况有8种对应变换,常用的为DCT-II变换,公式如下
X(k)=\sum_{n=0}^{N-1}x[n]\cos\left[\frac \pi{N}(n+\frac{1}2)k\right]mel频谱经过DCT变换后得到倒谱系数(cepstral coeffs)即MFCCs。
能量和delta的计算属于mfcc特征体系下的可选操作。
能量特征相当于给mfcc加上bias偏置,具有一定抗噪作用,公式如下
energy=\sum_{n=1}^N x^2[n] =\frac{1}{N}\sum_{m=1}^N |X[m]|^2根据公式,可以从时域计算,也可以基于频域计算,很明显,这样计算出的结果动态范围太小,一般针对结果取log运算即energy=\log(\sum_{n=1}^N x^2[n] ) ,又称log能量,可以替换首个mfcc直流分量值或首位置追加。
delta是计算数据的变化,基于当前点区域的局部斜率最小二乘近似值,公式如下
delta=\cfrac{\sum_{k=-M}^Mkx[k]}{\sum_{k=-M}^Mk^2}M为阶数,为奇数,一般取9
针对mfcc计算其delta,然后再计算delta的delta,可以侦测mfcc状态的变化,变化的变化,可以作为mfcc的两组辅助特征参与网络模型的训练,某些情况下起到更好的准确性和泛化能力。
mfcc相关效果图如下
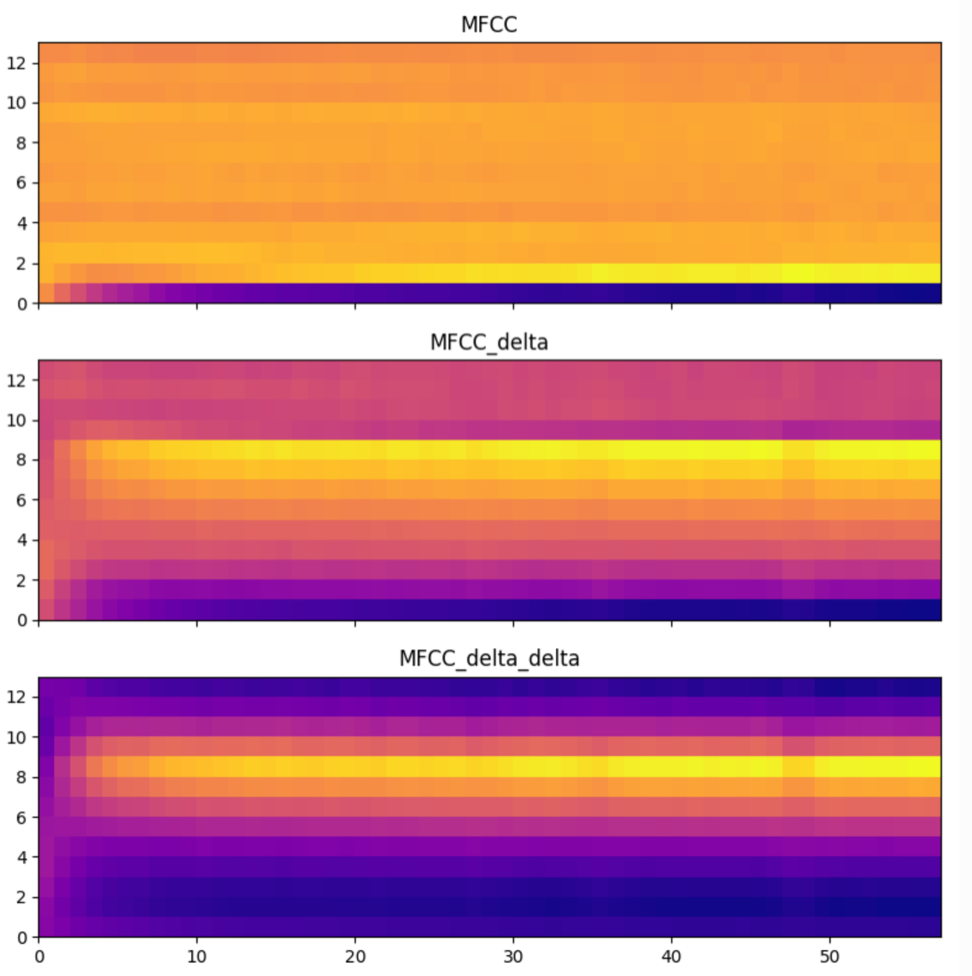
综上所有,详细描述解释了算法流程中每一步计算流程,下面将对一些步骤流程涉及到的细节思考点和延伸点做深入的展开。
针对上面预加重方式而言,本质上是一个高通滤波器,是衰减低频的,本身并不会提升高频,“补偿高频分量损失,提升高频分量”并不太严谨但比较形象,衰减低频相对来说就是变相提升高频,是缩减高低频动态范围的。
为什么要缩减高低频动态范围,有没有更好的方式,答案就是weight-A计权。
上面有提到“人耳对低频比较敏感,高频不太敏感”,这个敏感是针对频率分辨而言的,针对频率的强度而言,这句话是反过来的即人耳对高频比较敏感,低频不太敏感,以吉他乐器为例,用同样力度拨最粗和最细的弦发出的音,即物理上两者强度(振幅)是一样的,但听觉上高频比低频要响的多,人们用weight-A计权来量化这种“响度”的心理指标,数学上表示不同频段的log函数加减,效果如下图。
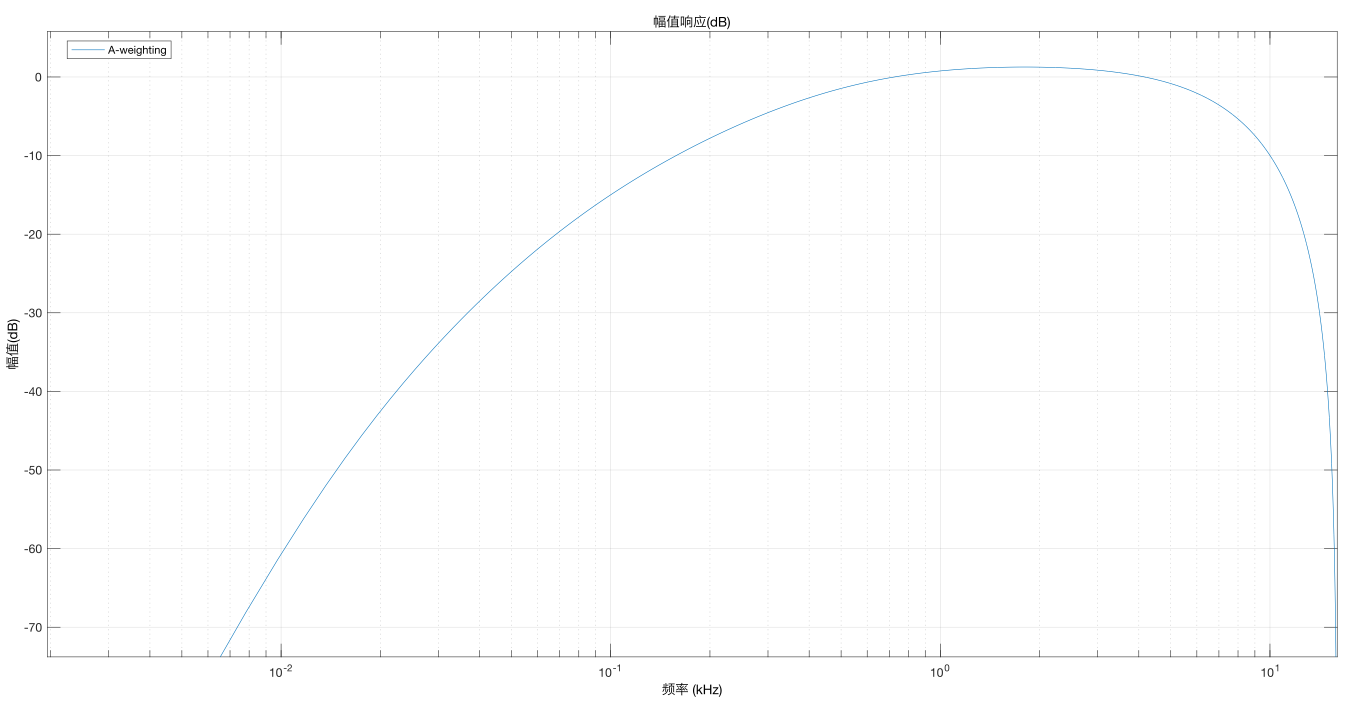
如图所示,整个频段不仅有衰减、还有真正的提升区域。
针对一些业务的深度学习模型训练,加weight-A计权能提升4%~5%左右精度。
数据分帧涉及到帧长和重叠两个问题,帧长决定频域的频率分辨率和时域的时间分辨率,帧长越长,频域分辨率越精确,时域分辨率越模糊,但受限大多数信号本身非平稳特点不可能无限长,帧长越短,时域分辨率越精确,频域分辨率越模糊。
重叠问题,就是相对当前帧滑动的问题,如上面分帧流程所述一般情况下滑动帧长的1/4或1/2,当然,滑动长度也可以等同帧长(前后重叠为0),甚至超过帧长(没有重叠,前后跳跃)。
重叠多少还是不重叠还是跳跃,本身并不会提升时域分辨率,可以理解为频谱t维度的不同时间间隔采样,滑动小相当于频谱图的插值升采样,滑动大相当于频谱图的抽取降采样,针对端点侦测业务频域的相关算法,滑动太小或跳动过大都不会有好的效果,如下面效果对比。
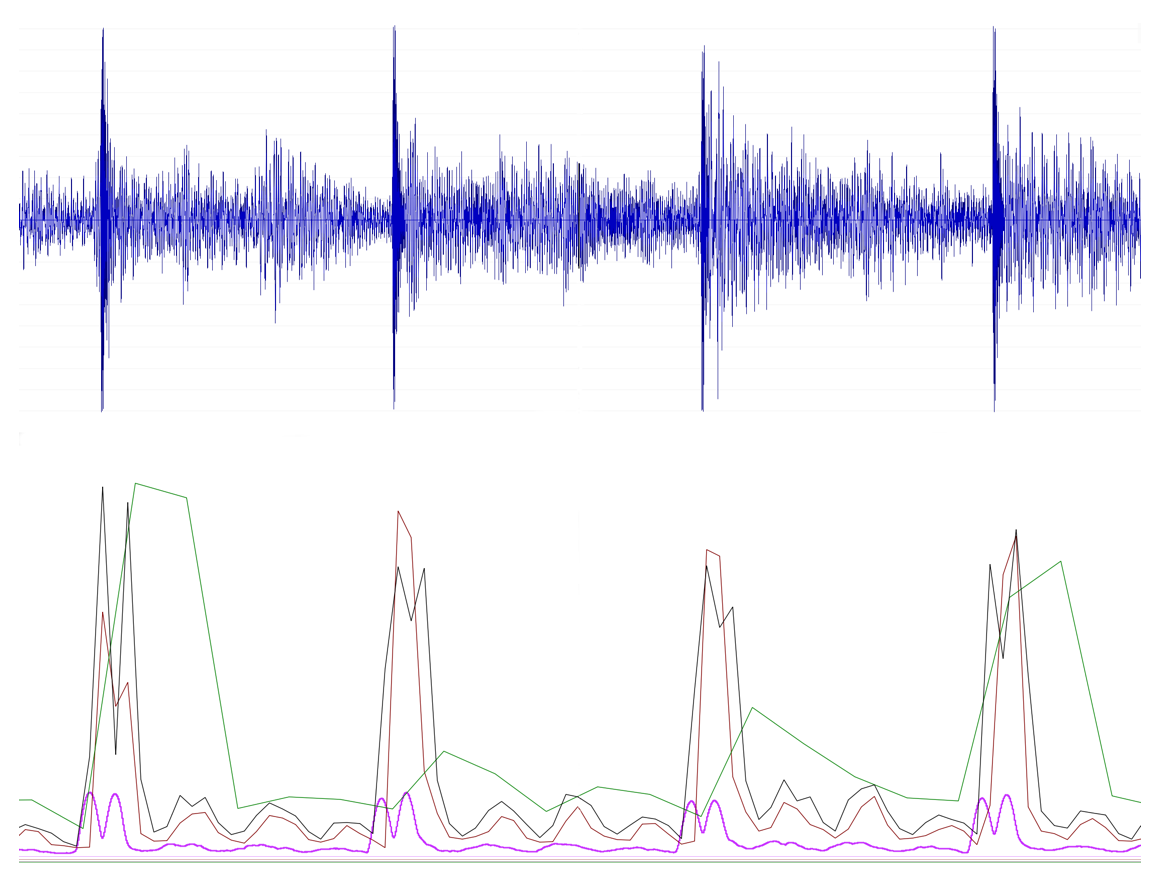
如图所见,紫色和绿色是滑动极小和跳动过大效果。
针对端点侦测相关业务,选择合适帧长后,前后滑动一般没有重叠或少许跳动效果相对好一些。
时域加窗目的是减少频谱泄露,上述算法流程描述中,一般情况下加Hann窗,但窗函数有很多,如Triang,Hann,Hamm,Guass,Kaiser,Flattop,Blackman等等。
不同窗如何选择,在深度学习一些业务中,不同窗的选择对模型的训练和结果影响是怎样的,或者哪些窗在业务中是值得做尝试的。
Guass,Kaiser非常值得尝试,公式如下
\begin{cases} guass(n)=e^{-n^2/2\sigma^2} =e^{ -\frac12 \left( \alpha \frac{n}{ (N-1)/2 } \right)^2} , -(N-1)/2 \le n \le (N-1)/2 \\ kaiser(n)=\cfrac {I_0 \left( \beta \sqrt{1- \left( { \cfrac {n-N/2}{N/2} } \right)^2 } \right) } {I_0(\beta)} , 0 \le n \le N \end{cases}针对Guass:
\sigma=(N-1)/(2\alpha) , 两者之间互为反比undefined 默认\alpha=2.5
针对Kaiser:
I_0(\beta) 为零阶第一类修正贝塞尔函数,可有下面公式级数计算, I_0(\beta)=1+\sum_{k=1}^{\infty} \left[ \cfrac1{k!} \left (\cfrac \beta 2 \right)^k \right] ^2 ,一般取$15$项左右undefined 默认\beta=5
Gauss,Kaiser相比其它大多数窗而言,属于窗口可变窗,一般窗口宽度越大,分辨率越细,过渡带越小,但阻带衰减偏大;一般窗口宽度越窄,分辨率越大,过渡带越大,但阻带衰减偏小。
针对Guass和Kaiser这两种可以调整宽度的窗,在一些业务中可以选择最大化旁瓣衰减,用相应的频谱特征训练深度学习业务模型时,可能会有不错的表现。
上述算法流程描述中,一般而言5、6步合到一起是标准的频谱呈现结果,但从功率频谱非线性校正角度而言,
不止log函数一种,当然log是最重要最常用的一种,可以用cubic root(三次开方),类Relu等其它方式。
从深度学习角度来看,可以把类mel频谱当做一种网络层计算,log、cubic root等非线性操作当做激活函数。
从这个角度来看,针对不同的业务,激活函数的不同选择设计,对模型的训练和结果的影响有可能是天翻地覆的,在研发业务中是很值得关注测试的一个点。
mel频谱如此知名,难道做音频领域深度学习就只有mel频谱?当然不是,有些情况mel频谱不一定是最优的。
如上面算法流程描述中mel刻度的解释,是一种基于人耳听觉设计的log压缩刻度,后面发展出更准确人耳听觉模型刻度,Bark和ERB刻度,公式如下
bark=\frac{26.81hz}{1960+hz}-0.53, \quad hz=1960(\frac{bark+0.53}{26.81-bark})\quad erb=A\log_{10}{(1+0.00437hz)}, \quad hz=\frac{10^{\frac{erb}A}-1}{0.00437}A=\frac{1000\ln(10)}{(24.7)(4.37)}公式中 at^{n-1}e^{-2\pi bt} 部分为 \Gamma 形式函数,\cos 理解为tone,称之为gammatone。
一般情况下,人耳听觉模型中的ERB刻度和gammatone filter的bandwidth相关联,即b为ERB刻度的bandwidth。
基于这个滤波器求频响非常复杂,只能给出近似公式,论文公式推导足足有20多页,已超过大部分人的研究上限,即使拿论文的结果公式直接编程实现也不轻松。幸运的是audioFlux开源项目有比较标准的实现,感兴趣的朋友可以研究一下。
除了上述刻度以外,还有基于乐音八度的octave刻度,更通用的log刻度等等,基于上面算法流程,mel刻度产生mel频谱和mfcc特征,同样的流程,bark/erb等刻度产生对应的bark/erb频谱和相应倒谱系数,一些不同刻度频谱的对比图如下
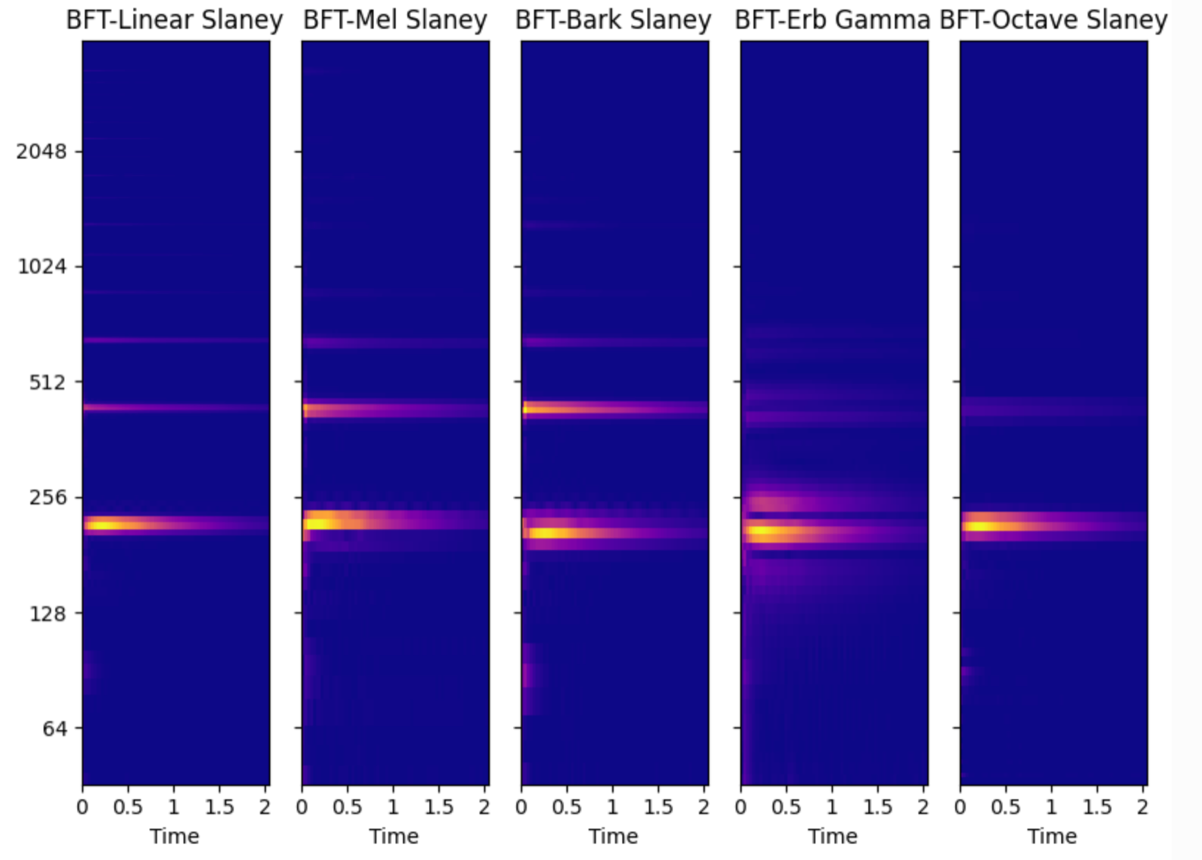
更多的不同刻度频谱类型可尝试使用audioFlux库测试。
在一些业务中,比如乐器相关业务中,上面所有的刻度中,可能都会有一些小问题,针对低频的频带,可能有些已经小于STFT的最小分辨率,这时候显然没意义,额外的造成干涉发散效果;针对中频的频带,有些可能过大,分辨不够细;针对高频的频带,可能还不够大,分辨还是相对过小。
上述情况下,在一些业务中,特定的一些网络结构中,中低频的分辨率差可能会导致训练模型的欠拟合,很难达到一定准确度,或者高频的分辨率过小可能会导致训练模型的欠拟合,泛化能力差,出现这种情况后可以尝试以下方式:
1,适当的增加数据集、调整网络结构和参数等通用方式。
2,增加不同维度的特征输入,让网络找到最优解或跳出局部最优解。
3,自定义刻度,既然明确原因,从特征本身优化上入手。
综上,不同scale下产生的频谱数据高低频细节、能量聚集、对比度都会有不同的差异,这种差异放大到一些业务实践中,模型的准确度和鲁棒性怎么样,就非常有尝试研究价值。
在深度学习一些业务中,如果mel刻度下的相关特征可以出结果,使用bark相关特征替换,往往有一定的效果提升。
数字信号中,滤波器有基础的高通滤波器和低通滤波器, 带通滤波器可以有低通和高通串联而成,Filter bank可以理解为多个带通滤波器。
滤波器组是一个映射矩阵,表示STFT线性频带和不同刻度下的频带映射关系,至于怎么映射,就是算法流程描述第5步中的三角窗函数法,三角窗的Filter bank如下图所示
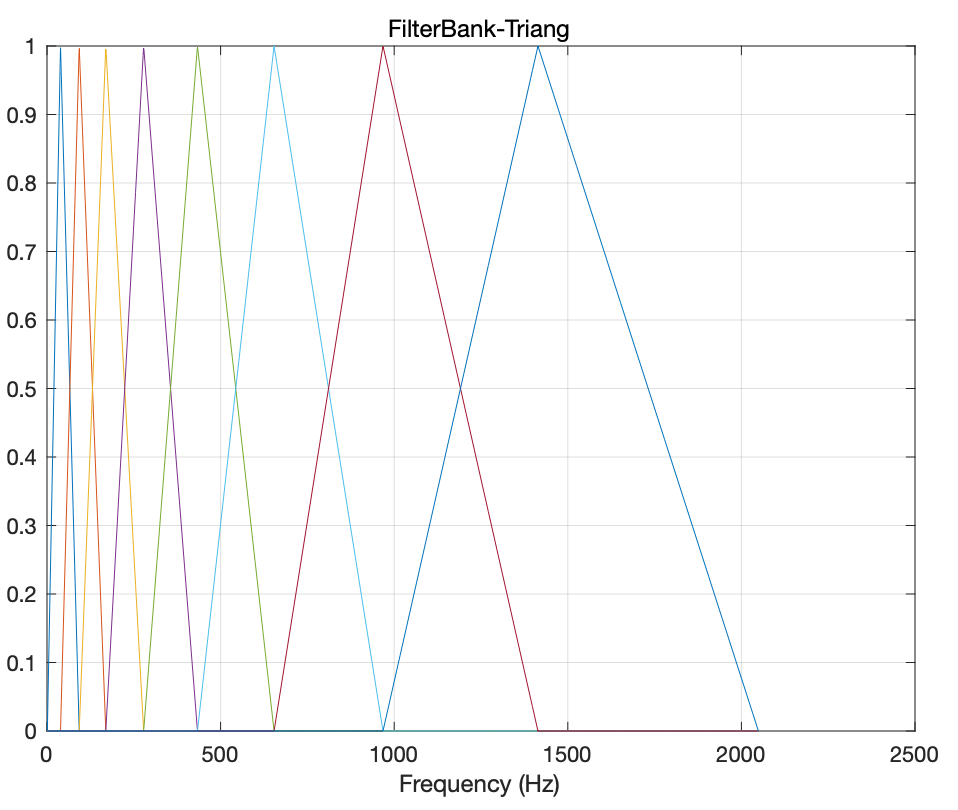
如上图所示,一般刻度产生的频带,低频带宽小,高频越来越大,意味着高频区域很长的一段频带都会参与当前频率分量的映射计算,相对低频而言显然不太合理,这时候需要对Filter bank进行归一化处理。
归一化方式有以带宽和面积区域两种方式,以带宽方式归一化效果如下图
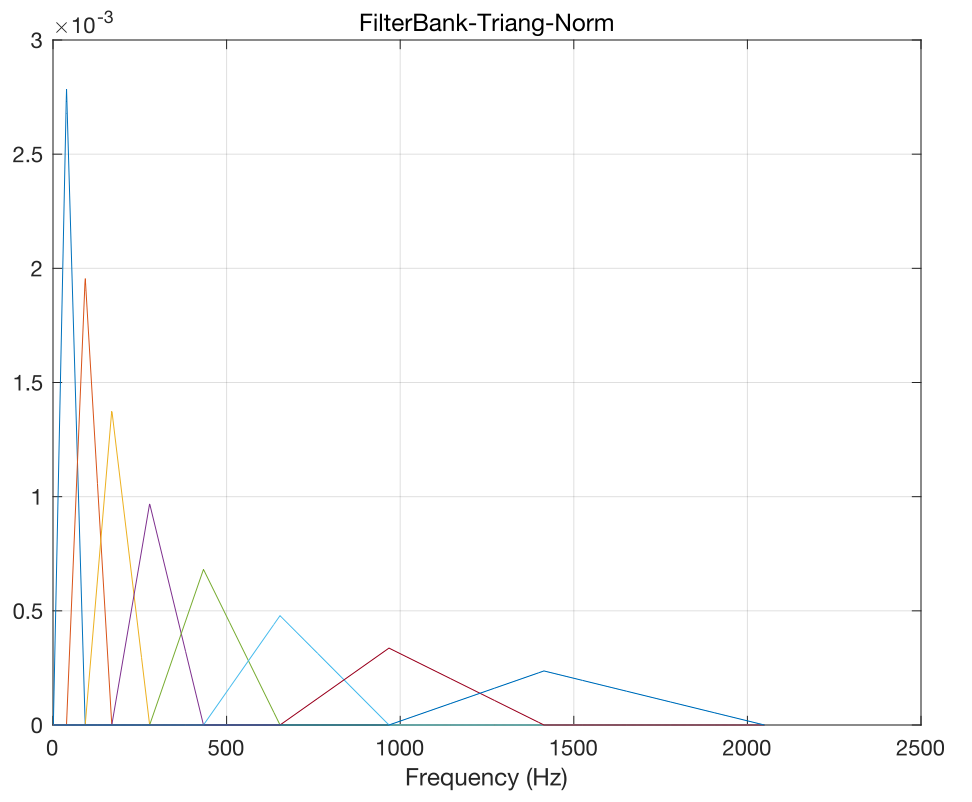
针对Filter bank的计算,难道就只有三角窗函数法,当然不是,可以使用Rect,Hann,Hamm等等这些窗函数,Gammatone也是一种特殊的窗函数,某种角度上讲甚至可以不计算,下面是几种不同窗下Filter bank的对比图
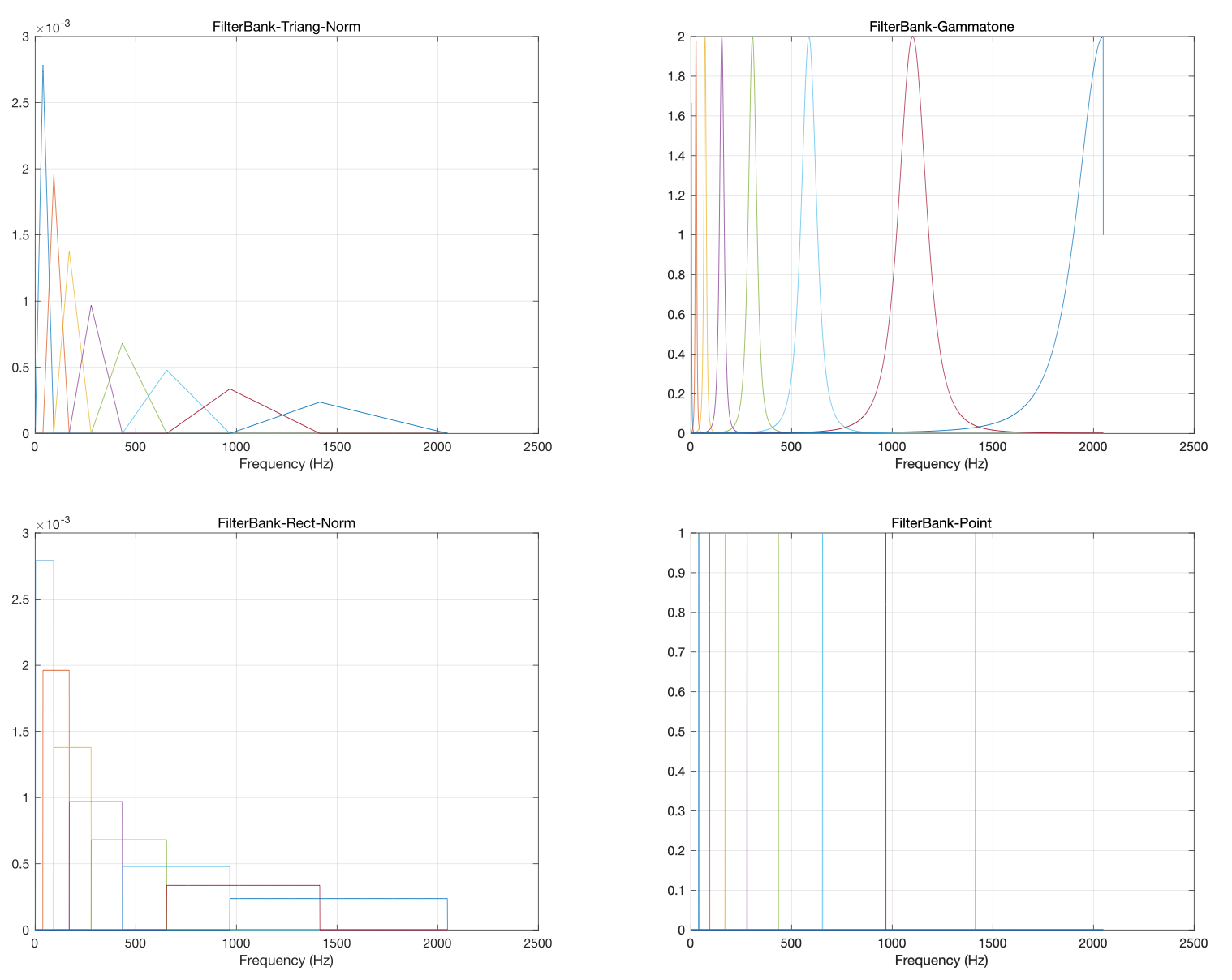
下面是不同窗下的频谱对比图
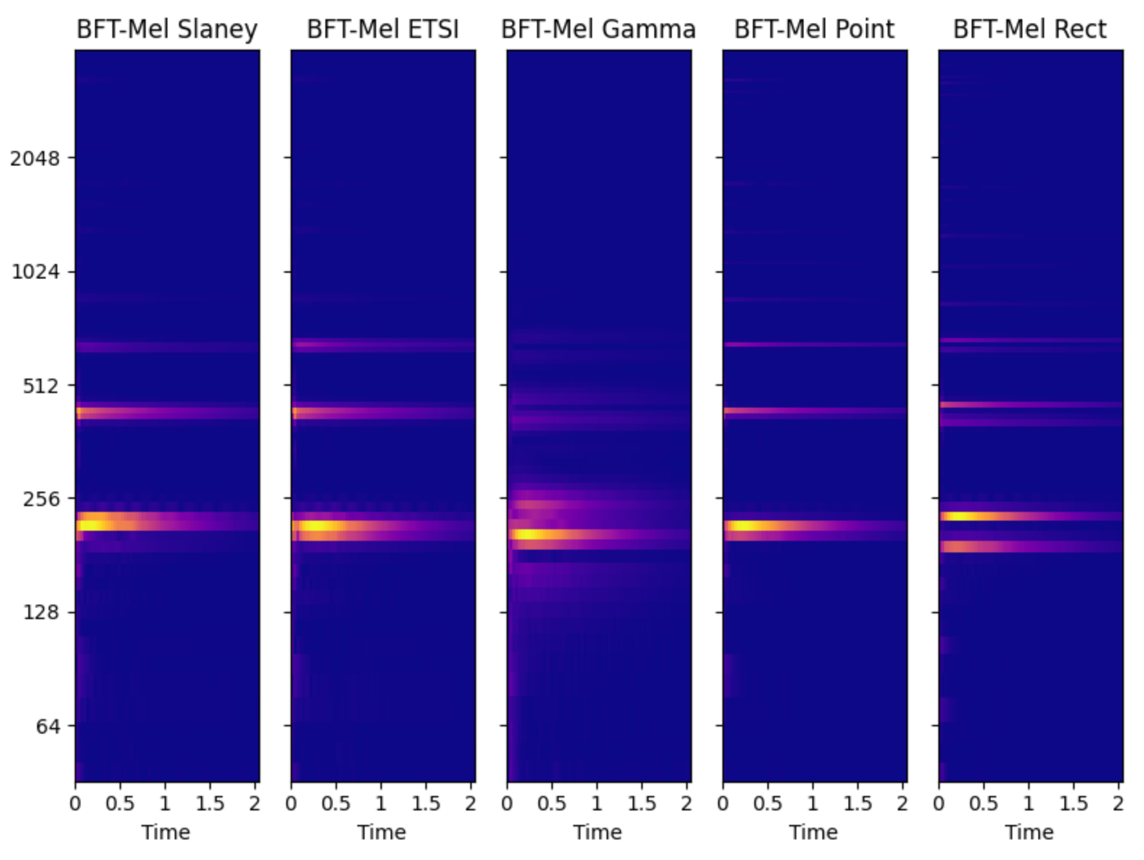
图中Slaney和ETSI是两种不同类型的三角窗,其它更多窗类型测试可尝试使用audioFlux库。
窗函数重叠处处理有很多细化方式,频带前后窗都是有重叠的,一般的处理方式是重叠点后面不再参与之前计算,重叠点之前不再参与之后计算,如下面图所示

如果各个频带窗函数可以等比例缩放,这样的话对不同刻度下的频带都变成可调整的,窗函数不同的宽度选择,对应时频分辨率不同的变化,结合PWT(伪小波变换),就是另外一种CWT效果的同等变体,不同于CWT对波函数的限定要求,可以用更广泛的窗函数研究CWT。
综上,针对Filter bank的计算,加什么窗?怎么加窗?何种归一化方式?使用这些组合产生出更多细粒度的不同特征,训练出模型准确性和鲁棒性如何,是非常值得尝试研究的。
什么是倒谱系数,为什么DCT计算后是倒谱系数?
倒谱的标准公式定义如下
C(r)=F\{\log(F\{f(t)\})\}数据经过FFT变换后取log后,再次FFT变换一般称为倒谱,更广义的讲即时域数据经过FFT变为频域数据,频域数据再次
FFT变换即倒谱变换。
DCT是DFT的特例,所以DCT针对之前FFT结果再次变换符合上述公式概念定义,也称倒谱系数;相比DFT,DCT能量较聚集,相当于频谱数据的再压缩,用小部分系数就能反映出数据的高度去相关的特征。
倒谱可以干什么?
可以估算音高,可以作为解卷积(deconv)的一种方式,分离信号,计算包络(envelope)/共振峰(Formant)等等,
解卷积推导公式如下
\begin{cases} x(t)=g(t)*h(t) \\ F\{x(t)\}=X(\omega)=G(\omega)H(\omega) \\ \log X(\omega)=\hat X(\omega)=\hat G(\omega)+\hat H(\omega) \\ F^{-1}\{\hat X(\omega)\}=\hat x(k)=\hat g(k)+\hat h(k) \end{cases}分数傅里叶变换(FRFT)
根据倒谱的定义,延展一下,能否多次FFT,多次FFT的意义是什么,多次变换引申如下
F^2=F(F(x))F^n(x)=F^{(n-1)}(F(x))设n=\frac{2\phi}\pi ,换元后定义
F_\phi(x)=F^{2\phi/\pi}(x)引用$\phi$后,FFT变换的次数可以非整数即分数傅里叶变换,物理意义的表现就是旋转频谱一定角度,可以多一个维度分析频谱,同时也带来其它概念的延伸,如分数卷积等等。
曾经看到国外有一个做音频分类的一个小业务,网络输入包括时域的能量、均方根、过零率、均值、方差、协方差、偏度、峰度、矩、中值、中位数、相关系数等等数十种时域相关的统计特征,不管三七二十一,合理归一化后,扔给一个卷积网络跑模型训练,最后能达到90%以上准确率。
这种方式不能说是好还是坏,从业务结果上来说,把网络完全当做一个黑箱,输入尽可能多的自身掌握的各种特征,打好标签,扔给网络跑,只要能出结果就是好的。
如果把这种操作延展,在音频领域特征选择上,一个体系的、全面的、多维度的任意不同粒度组合成一个灵活的大的特征数据,相对单一或少量组合的特征,作为网络输入训练模型是否更具有优势,这个问题是值得思考研究的。
针对大特征数据的训练,有以下几种方式可以尝试:
1,大特征数据合理归一化整体作为输入,单一输入,经典网络和不同网络结构组合训练。
2,大特征数据合理归一化整体作为输入,同样数据多路输入,各种不同网络结构组合训练。
3,大特征数据不同的特征维度,不同数据多路输入,分别走相同的网络结构和不同的网络结构组合训练。
4,基于第3种方式,一些特征直接作为中间隐藏数据插入内部不同网络结构中组合训练。
深度学习中,全连接、卷积、RNN等这些基础网络,在空间和时间维度上不同的细化神经元线性运算加各种非线性激活操作来完善自身通识的算法体系,解耦数据特征工程、特征建模和目标结果的层层依赖,成为一种通识的算法思维。传统基于统计学的机器学习和模式识别在此面前显得不堪一击,像一个暴发户一样,前人们含辛茹苦积累数十年的领域经验,一个门外汉几天就给颠覆了,关键是结果还比你好。
当然,从学习研究角度来看,如HMM、GMM、CRF等这些前人积累的经典算法模型,在后续业务中有可能用不到,但这些算法思维是很值得借鉴学习的,备足思维“原料”,任何时候都不过时。
这些网络的根在哪里,从算法角度来看就是数值计算和数值优化,数值计算层面网络里有大量的线代运算,自然有CUDA和各种BLAS作为支撑,最优化理论上,大部分情况下是训练收敛快慢、震荡的问题,相关理论研究积累目前来看相对成熟。
从工程角度来看,基于最速下降体系的反向传播算法已成事实上的标准,其它诸如二阶求导、牛顿法等始终为小众市场,但问题是自动微分工程上的实践,有pytorch在手,实现各种网络结构、自定义各种网络结构等算法难度上呈指数级下降,现在的玩法更多是网络的深度,网络的各种组合上,这可能才是目前网络的根结所在。
现在,回归到内嵌式网络训练 ,这些基础的网络本质上可以看做是积分变换,而音频领域有数十种经典的积分变换,这些变换不同于前人积累的特定领域的经典模型算法,它本身就是典型的高度抽象的数学公式,自带通识基础。
第一种方式
拿最常见的mel频谱来说,姑且认为它是STFT变换的一种,我们可以直接拿mel频谱当做网络输入训练,同样的,我们可以把mel频谱写入网络结构的前向计算中,这时可以直接拿时域数据当做网络输入训练,这两者之间的差别在哪,答案是没有差别,之前是mel频谱作为特征输入,现在只不过不是mel频谱的计算放在网络开头计算而已,速度可能会快一些,叫一个更有逼格的名字,Mel-CNN、CWT-Transformer、NSGT-RNN、CRF-LSTM、PCA-Inception等等网络。
第二种方式
可以把mel频谱计算放到网络的中间,这时候mel频谱计算可以作为一个算子参与到前向、后向这些计算,影响前后神经元权重参数的更新,这时候可以称之为Mel-CNN等等总算是更进一步,更准确说是mel频谱激活函数。
第三种方式
mel频谱有自己的神经元,开始成为真正的mel频谱网络层,同样的延展,类如mel频谱等积分变换,什么都不操作,它就是一个稍微复杂点的算子、激活函数,如果在空间和时间维度上加上神经元设计,谁能保证不会出现下一个类卷积网络的通识结构呢,当然,这种设计要求有较强的理论推导能力和大量的基础测试,足以支撑构建新设计网络的理论基础和业务逻辑解释。
最后,音频领域数十种经典的积分变换加上传统机器学习的经典模型算法,如何内嵌式网络训练,最最起码视野开阔很多,对于业务而言,真正的网络层实现可能算是标准的科研,而作为一个算子激活函数的使用是应该尝试的,最不济,把这些当做不同维度的特征输入也总比什么都没有好,多一个维度,多一种特征,多一种选择。
本文大体上分四个部分,算法流程详细描述解释了每一步计算流程,相关细节算是简单步骤流程的细节点思考和延展,各种刻度、滤波器组、倒谱系数算是重要概念和重要步骤的细节点思考和延展,以上三个部分算是整个“深入”部分,方法论是“浅出”部分。
备足思维“原料”,任何时候都不过时
多一个维度,多一种特征,多一种选择