归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序,若将两个有序表合并成一个有序表,称为二路归并。
归并排序实际上就是将一个大的数组,通过递归后,化简成许多个小排序,再将小排序进行排序,最后再对小排序后的结果再次排序,以此类推。
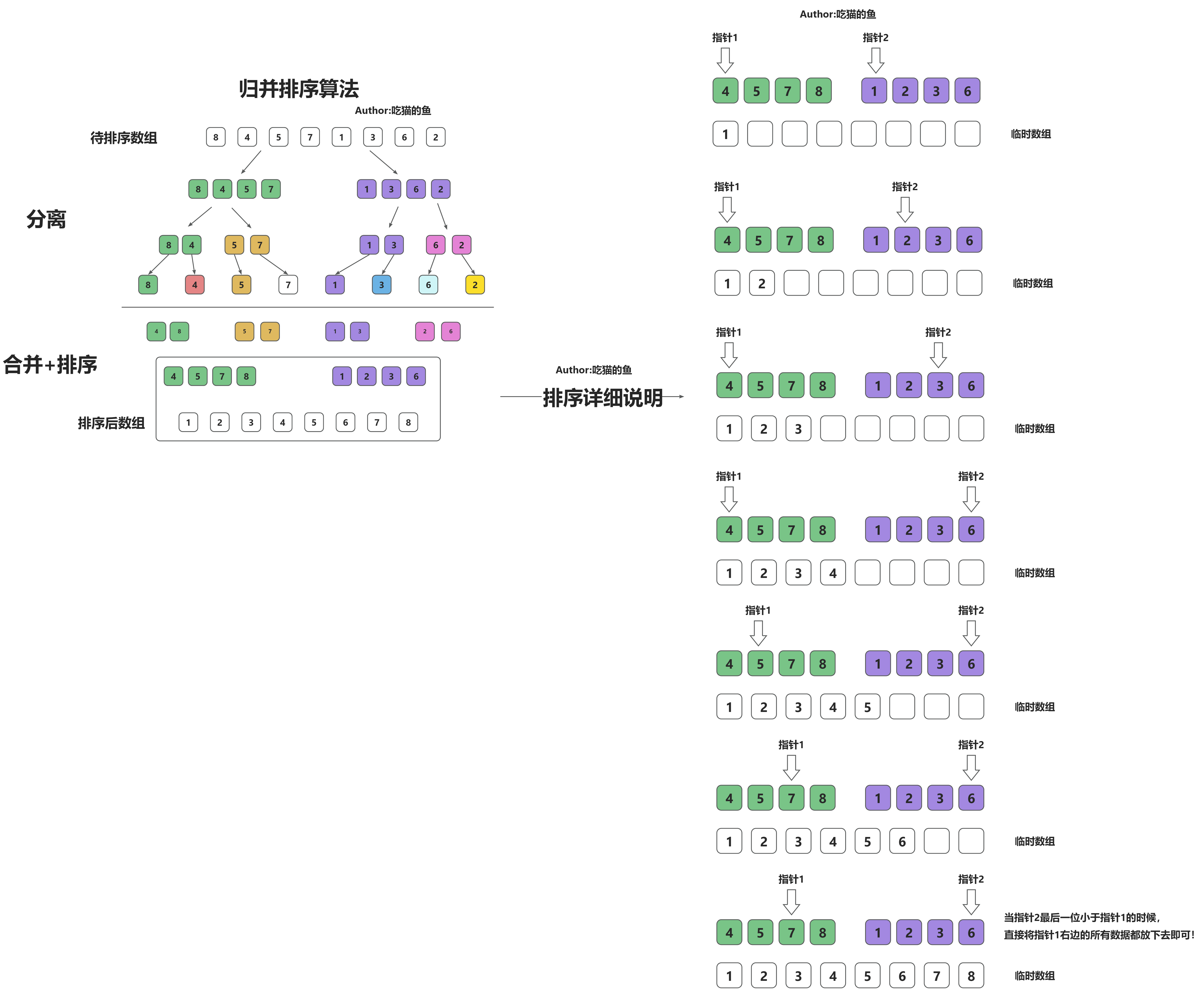
归并排序算法概览

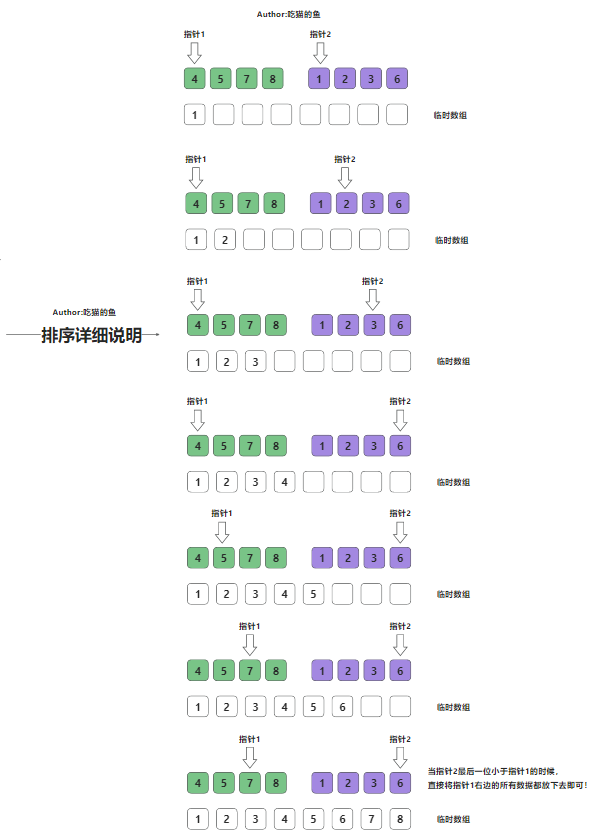
归并排序中排序的详细说明图
public class Merge {
//初始化辅助数组
private static Comparable[] assist;
//判断数字大小,true ab ;
private static boolean less(Comparable a,Comparable b){
return a.compareTo(b)<0;
}
//对数组进行排序
public static void sort(Comparable[] a){
//初始化assist数组
assist = new Comparable[a.length];
//建立最小索引和最大索引
int begin = 0;
int end = a.length-1;
//调用sort重载方法完成数组a中索引begin到end中的排序
sort(a,begin,end);
}
//开始将数组中begin到end进行排序
private static void sort(Comparable[] a,int begin,int end){
//做安全性校验
if(begin>=end){
return;
}
//对begin到end的数据进行分组
int mid = begin + (end - begin) / 2;
//对两边的数组进行排序
sort(a,begin,mid);
sort(a,mid+1,end);
//接下来对两组数据进行归并即可
merge(a,begin,mid,end);
}
//a数组中begin到mid为一组,mid+1到end为一组,将两组进行归并
private static void merge(Comparable[] a,int begin,int mid,int end){
//定义三个指针
int i=begin;
int p1=begin;
int p2=mid+1;
//遍历,移动p1指针和p2指针,比较对应索引处的值,找出小的哪个,放到辅助数组的对应索引处
while(p1<=mid && p2<=end){
//比较索引处的值
if(less(a[p1],a[p2])){
assist[i++] = a[p1++];
}else{
assist[i++] = a[p2++];
}
}
//遍历,如果p1的指针没有走完,那么顺序移动p1指针,把对应的元素放到辅助数据的对应索引处
while(p1<=mid){
assist[i++]=a[p1++];
}
//遍历,如果p2的指针没有走完,那么顺序移动p2指针,把对应的元素放到辅助数据的对应索引处
while(p2<=end){
assist[i++]=a[p2++];
}
//把辅助数组中的元素拷贝到原数组中
for(int index=begin;index<=end;index++){
a[index] = assist[index];
}
}
}优点:速度块(O(nlogn))
缺点:需要通过内存空间来换取,由于在执行过程中会产生多个临时数组来存储数据,所以比较消耗内存。
补充:需要注意的是,在上述代码中,为防止整数溢出问题的出现,在求中间的下标mid时,使用mid = begin + (end - begin) / 2;,而不是mid = (begin + end) / 2
本文共 656 个字数,平均阅读时长 ≈ 2分钟