原文:轻量级实时三维激光雷达SLAM,面向大规模城市环境自动驾驶

对于自动驾驶汽车来说,在未知环境中的实时定位和建图非常重要。本文提出了一种快速、轻量级的3D激光雷达SLAM,用于大规模城市环境中自动驾驶车辆的定位。文中提出了一种新的基于深度信息的编码方法,可以对具有不同分辨率的无序点云进行编码,避免了点云在二维平面上投影时丢失维度信息。通过根据编码的深度信息动态选择邻域点来修改主成分分析(PCA),以更少的时间消耗来拟合局部平面。阈值和特征点的数量根据距离间隔自适应,从而提取出稀疏的特征点并均匀分布在三维空间中。提取的关键特征点提高了里程计的准确性,并加快了点云的对齐。在KITTI和MVSECD上验证了该算法的有效性和鲁棒性。里程计估计的快速运行时间为21ms。与KITTI的几种典型的最先进方法相比,所提出的方法将平移误差减少了至少19%,旋转误差减少了7.1%。
作为自动驾驶的核心技术之一[1],车辆定位和导航一直是研究热点。该算法需要处理大量数据[2],轻量级算法尤为重要。这些技术对汽车工业具有重要价值[3]。定位和导航通常可以通过高清地图和GPS实现。然而,高清地图和GPS并不适用于所有城市场景,例如隧道、天桥、高楼屏蔽和技术问题导致的服务中断。在没有高清地图和GPS的情况下,定位可以通过SLAM的自我运动估计来解决。稳定的技术算法可以为自动驾驶提供了安全性[4]。SLAM能够解决未知环境中车辆的位置估计问题,并构建周围环境的地图。根据使用的传感器(摄像机、激光雷达),通常可以通过视觉SLAM[5]、[6]、[7]和激光雷达SLAM[8]、[9]、[10]、[11]、[12]对其进行分类。视觉SLAM被动地从相机获取信息,受周围环境的照明和纹理条件的影响很大。相比之下,3D激光雷达SLAM依赖于激光雷达对环境几何信息的主动测量,而不是纹理信息。因此,LiDAR SLAM更为稳定,并广泛应用于户外场景的实际应用。完整的激光雷达SLAM系统包括前端的姿态估计里程计和后端的全局姿态图优化。点云配准是前端的核心,从中可以获得车辆姿态。典型的方法包括迭代最近点(ICP)[13]、归一化分布变换(NDT)[14]和基于特征的方法。经典ICP基于欧氏距离对最近点进行配对,并以迭代方式不断优化点对点对应关系,以获得车辆的运动变换。然而,帧点云中每对点的变换需要大量的计算。NDT将点云划分为许多小网格,然后计算网格之间的概率分布。连续可微概率密度用于估计连续LiDAR帧之间的自主运动。然而,该算法对旋转角度敏感,并且配准精度受网格大小的影响。基于特征的方法仅提取具有特征的点云进行匹配,以实现出色的实时性能和高精度。然而,在几何特征不明显的城市场景中,自动驾驶汽车的特征提取方法仍然是一个挑战。
基于上述方法,已经提出了几种户外3D激光雷达SLAM方法。LOAM[8]提出了基于特征点的点云点对线和点对面配准,以实现精确的里程计。然而,由于缺乏后端优化,在大规模环境几乎没有几何特征的情况下,它产生了显著的漂移。LeGO LOAM[9]提出了一种利用地面优化的快速、轻量级SLAM方法,但缺少地面点云会给里程计带来更多误差。HDL_GRAPH_SLAM[10]是一种基于带回环的图形优化的3D激光雷达SLAM框架,可以融合IMU、GPS和道路约束等,但前端里程计的scan-to-scan点云配准方法不够精确。LIOM[11]在大规模快速移动环境中提出了一种低漂移、鲁棒的LiDAR惯性里程计和建图方法,但它占用了大量内存,时间性能较差。这些解决方案在大规模城市环境中仍然存在缺陷。
在本文中,我们关注复杂的大规模城市环境中自动驾驶车辆的鲁棒实时定位和建图。通过基于平面拟合删除地面点,可以减少输入点云的数量。然后根据深度信息对预处理的无序点云进行编码,而不是投影到2D平面上。通过改进PCA,提出了一种基于编码深度信息的鲁棒双自适应特征提取算法。通过配准提取的边缘和平面点来估计车辆的姿态。最后,使用两步循环检测来优化全局图,消除累积误差。我们的系统的有效性和鲁棒性已在数据集KITTI[15]和MVSECD[16]上得到验证。本文的主要贡献如下:
在三维激光雷达SLAM中,姿态估计主要通过帧间的点云配准来完成。SLAM中的公共点云配准包括ICP[13]直接配准和特征点配准。ICP不需要对输入点云进行排序,只需要找到要配准的最近点,但对每个点进行配准需要花费大量时间。基于特征点的方法需要对输入的无序点云进行排序,但可以快速配准。
经典ICP迭代解决了point-to-point transformation。为了提高点云配准的速度和精度,将配准点到平面的距离作为误差度量,将点与局部平面配对。GICP[17]通过结合点到平面ICP和平面到平面ICP方法,通过两个局部平面之间的匹配修改了损失模型。IMLS-SLAM[18]提出了一种基于隐式移动最小二乘的点对模型对齐方法,该方法通过提取可观察的采样点将采样点与隐式表面对齐。这些工作在一定程度上改善了ICP,但当处理大量点云数据时,实时性能仍会受到影响。
与ICP方法不同,特征点方法只配准少量提取的特征点,因此配准速度快。LOAM[8]是一种经典的室外3D激光雷达SLAM,它首次提出了一种基于特征点配准的方法。根据激光雷达的角度分辨率对输入点云进行排序。LOAM计算同一直线束上几个相邻点云的平滑度,以提取边缘特征和平面特征,并优化点对线和点对平面距离残差,以获得里程计姿态。在LOAM的基础上,LeGO LOAM[9]提出了一种轻量级SLAM系统。它通过将点云投影为距离图像(distance images)来对输入的无序点云进行排序。然后,对分割的地面点和边缘点进行两步L-M非线性优化,并依次求解两组点云的变换系数。然而,将点云投影到二维平面上将丢失一个维度信息。Lio-sam[19]是一种基于特征点的融合方法,结合了IMU和GPS数据,但需要传感器的联合校准。F-loam[20]在不同距离提取相同数量的特征点,与上述几项工作相同。它采用了一种非迭代的两步畸变补偿来代替迭代畸变补偿,提供了高的计算效率和精确的姿态。MULLS[21]提出了基于分类特征点的多尺度线性最小二乘迭代最近点算法。
主成分分析(PCA)方法用于提取六个精细特征,包括ground points, facade, roof pillar, beam和vertex。将特征点分类用于点对点、点对线和点对平面ICP配准,获得低漂移和多用途的LiDAR SLAM系统。
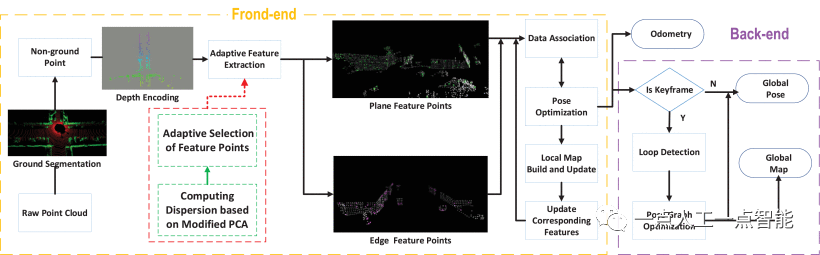
本文提出的系统框架如图1所示,其中,前端从传感器获取点云数据,并对原始点云进行预处理以分割地面点。使用深度信息对非地面点进行排序。通过自适应提取方法从非地面点提取边缘和平面特征。基于两个连续帧中特征点的对齐,获得车辆运动的相对姿态。车辆的里程计可以通过累积时间上的相对位置来估计。后端从里程计接收位置信息并判断车辆是否已到达其先前位置。最后,使用基于图的优化方法来消除匹配过程中的误差,以获得全局一致的轨迹和建图。
地面点通常占据自动驾驶车辆记录的3D点云的很大比例。通过对输入点云进行地面分割,可以减少点云的数量。传统的地面分割方法包括RANSAC[22]和射线地面滤波方法(the ray ground filter)[23]。RANSAC通过观测数据的随机样本估计模型参数。射线地面滤波算法计算同一角度上点半径的变化以获取地面点。然而,上述算法从整个点云中随机选择点,导致运行时间缓慢和分割错误。
在本文中,我们采用了一种快速地面滤波方法[24],该方法选择种子点集作为先验值,以加快算法的速度。
首先,沿着车辆的移动方向将点云框架划分为n个段。x轴方向上的区域被划分为多个子平面。将多个子平面合并为一个平面,以减少地面坡度变化带来的分割误差。然后,我们沿着z轴选择具有较小值的点,并计算它们的平均高度H_m 。th_z 指选择种子点的阈值。当点的z 值小于阈值H_m+th_z 时,选择该点作为种子点集S \in \mathbb{R}^3 。种子点作为初始平面的优先点,用来加速平面拟合。种子点集被拟合到初始平面中。计算每个点与初始平面之间的交叉投影距离。如图2(a)所示,如果距离小于人工阈值th_g ,则该点将被视为地面点(the ground point)。

用于估算平面模型的数学表达式如下:
ax+by+cz+d=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)
表示为矢量形式:
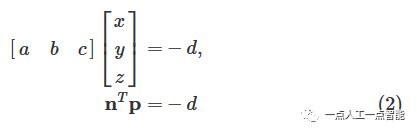
\pmb{\text{n}} 由协方差M\in \mathbb{R}^{3\times3} 求解,M 描述每个子区域的种子点集的色散度(Dispersion):
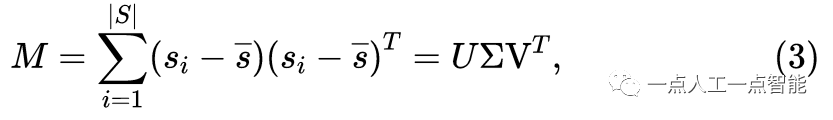
其中\bar{s}\in \mathbb{R}^3 是所有点s_i \in \mathbb{R}^3 的平均值,s_i \in \mathbb{R}^3 ,U \in \mathbb{R}^{3\times 3} ,V = MM^T ,V\in \mathbb{R}^{3\times3} ,\Sigma = \text{diag}(\sigma_1,\sigma_2,\sigma_3) 。法线\pmb{\text{n}} 垂直于平面,表示方差最小的方向。参数d 可以通过将方程(1)中的\pmb{\text{p}} 替换为\bar{s} 来求解。通过计算每个点与初始平面之间的垂直距离,与阈值Th_{dist} 进行比较来判断其是否属于下一平面。最后,将分类后的所有地面点作为下一次迭代中的种子点集进行迭代优化。图2(b)显示了使用上述算法的子平面合并的地面点云。
从LiDAR获取的输入数据通常是无序的3D点云,可以通过投影到2D平面上或根据角度信息进行分类,将其转换为有组织的点云序列。这里,采用深度信息来对无序的输入点云进行排序,避免了维度信息的丢失或对激光雷达分辨率的依赖。3D scan在传感器坐标的径向上以相等的间隔分成N_r 个环。环数计算如下:
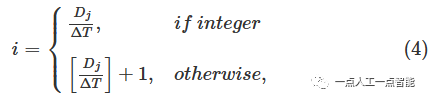
其中[⋅]是取整符号,\Delta T 是不同环之间的径向间隙距离,D_j 是每个非地面点云p^N_j(x_j,y_j,z_j) 的深度信息,由D_j=\sqrt{x_j^2+y^2_j+z^2_j} 计算。当间隔太大时,特征点分布稀疏,这影响了里程计的准确性。在本文中,我们使用\Delta T=4\ m 和N_r=21 。根据每个点的距离值D_j ,点p^N_j 被划分为相应的环N_j (如图3所示)。每个环的点云子集表示如下:
\rho=\bigcup_{i \in\left[N_{r}\right]} \rho_{i}\ \ \ \ \ \ \ \ (5)
其中\rho_i是属于第i个环的点集,N_r=[1,2,...,N_{r-1},N_r] 。
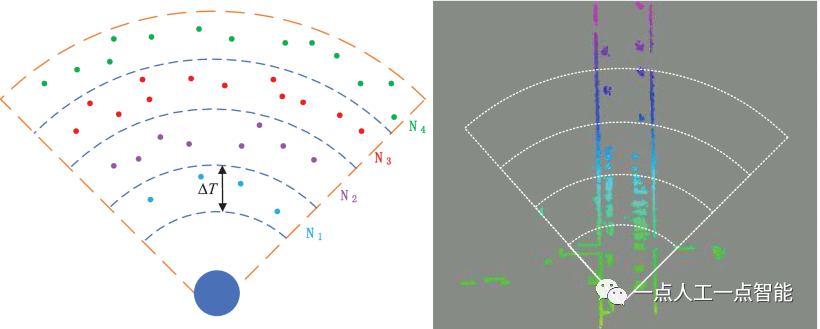
在点云被划分之后,每个环R(i) 由点云子集表示为:

因此,将点云分类为具有不同距离索引D_{id} 的集合,并且根据该索引对点云执行进一步处理。
由于在配准过程中没有匹配点,非地面点云中的奇异值点对里程计的定位精度有不利影响。因此,在特征提取之前需要去除奇异值点。通过对非地面点进行聚类,采用欧氏聚类方法对物体进行分类。当聚集点云的数量小于阈值时,将对异常值进行分类和删除。在特征提取之前去除异常值可以减少冗余点并增加特征点的可行性。
LOAM[8]提出了一种特征提取方法,以计算同一波束上几个相邻点的局部平滑度。但是,由于平滑度值相等,在几何退化情况下可能会失败。为了提高特征提取算法的鲁棒性,改进了主成分分析(PCA)算法来提取点云特征。在原始PCA算法中,使用固定数量的邻域点来拟合局部平面。我们通过距离间隔自适应地选择邻域点来拟合局部平面,从而改进了该方法。邻域点k 的数量定义为:k=\alpha -[\beta D_{id}(i)] ,其中[⋅]是取整符号,α和β是线性参数。为了降低搜索计算成本,将点云存储在3D KD树中。通过使用这些邻域点来计算局部域色散(The local domain dispersion)。选定的邻域点p_i(x_i,y_i,z_i) 与局部中心之间的距离为:
\partial _i =p_i-\frac{1}{k}\sum^{k}_{j=1}p_j=[\partial_{ix},\partial_{iy},\partial_{iz}] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7)
其中k 是邻域点的总数,i=1,2,3,...,k 。然后通过以下公式计算k 个点的协方差矩阵:
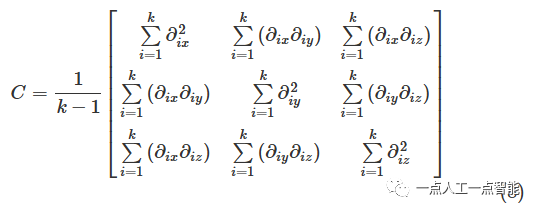
协方差矩阵C的特征值\lambda_i=(i=1,2,3) 和对应的特征向量\mathbb{N}_i(i=1,2,3) 通过奇异值分解(SVD)确定。对特征值进行排序以获得\lambda_1>\lambda_2>\lambda_3 。对应于最大特征值\lambda_1 的特征向量\mathbb{N}_1 是主向量,对应于\lambda_3 的特征向量\mathbb{N}_3 是法向量。这些特征值和特征向量可用于提取局部点云的边缘和平面特征。根据特征值之间的关系,局部线性和平面性可以定义为[25]:

其中\delta 是平面度,\epsilon 是线性度。根据\delta 和\epsilon 的值选择特征点。与原始PCA方法相比,改进的PCA算法加快了特征提取速度。使用邻域点(k=\alpha - [\beta D_{id}(i)],\alpha=10,\beta=0.1) 的自适应选择的特征提取比固定点(k=5) 快4ms。
通常,特征点的选择阈值与特征点的数量是固定的(例如,文献[8]选择20个边缘点)。然而,通过激光雷达扫描获得的点云在远距离稀疏,在近距离密集,导致特征点分布不均匀。不均匀分布对里程计的精度和SLAM系统的稳定性有不利影响。因此,我们提出了一种基于距离的特征点自适应选择方法。根据第4.3节,在编码阶段获得每个点云的索引D_{id} 。根据距离间隔自适应地计算特征点选择的阈值\mathcal{X} 为:
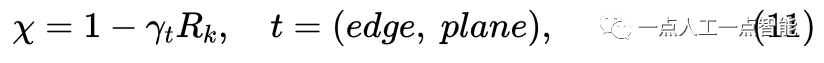
其中k 是每个点的距离,R_k 是通过等式(4)获得的距离数k 的范围,\gamma 是线性因子。通常,由于姿态估计需要更多的平面点,\gamma 平面的值设置为大于\gamma 边缘。如图4所示,根据方程(9)和(10),通过比较获得的阈值和局部色散值来选择边缘p_{\varepsilon} 和平面p_s 特征点:
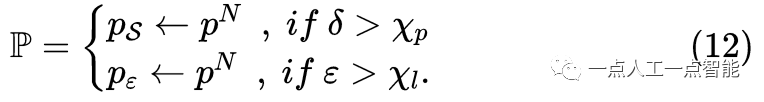
在不同的距离间隔中动态选择不同数量的特征点。特征点的自适应数量在数学上表示为:num=\omega_tR_t,\omega<1 ,num是整数。如图5所示,通过自适应选择方法获得的特征点比通过固定选择方法得到的特征点稀疏。提取的特征点在六个自由度上均匀分布。在六维空间中均匀分布的特征点给每个自由度带来了约束,并提高了里程计的精度和SLAM系统的稳定性。特征提取算法的完整过程如算法1所示。
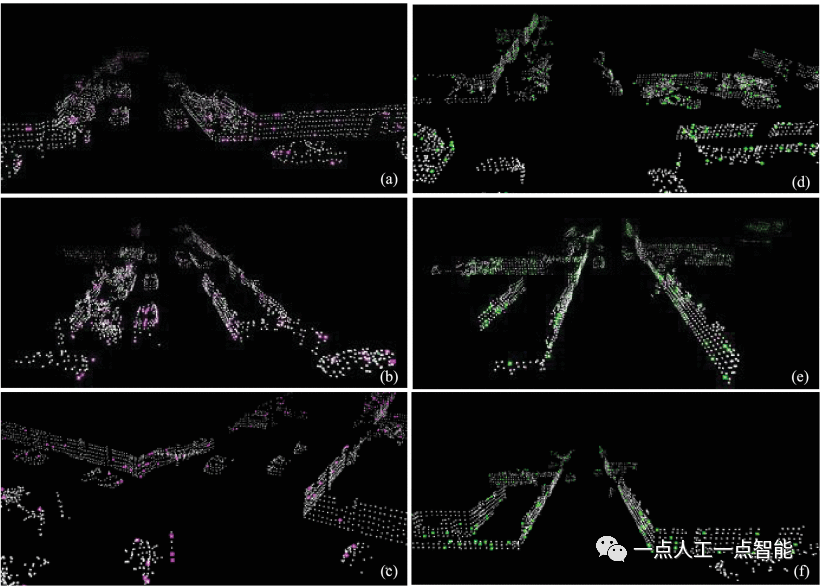


姿态估计是在全局地图的地面坐标中对齐当前边缘特征点和平面特征点。为了加快对应点的搜索速度,将边缘和平面特征点存储在KD树中。地面坐标系标记为\text w ,激光雷达坐标系标记\mathcal{L} 。车辆的状态转换关系可以表示为:

通过李代数,六个自由度的状态变换表示如下:
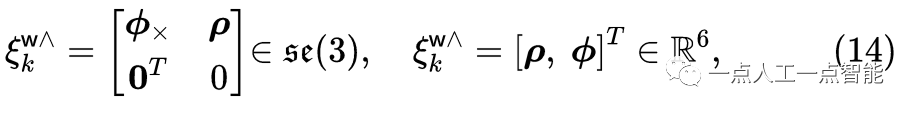
其中\rho 和\phi 分别表示切线向量中的相应平移和旋转,
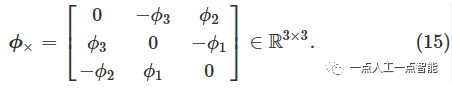
李代数和李群通过指数映射和对数映射进行变换[24]。李群T^{\text w}_{\mathcal{L}}=[\pmb{R,t}] \in SE(3) 的变换包含旋转矩阵\pmb{R}\in SO(3) 和平移向量\pmb{t}\in\mathbb{R}^3 。旋转矩阵和平移向量之间的映射关系为:
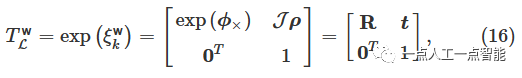
其中\mathcal{J} 是雅可比矩阵[26],其定义为:
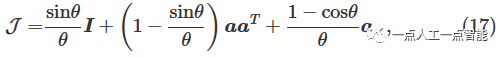
\theta是\xi^{\text w}_k 的模长度,\pmb{a} 是\xi^{\text w}_k 的方向向量,长度为1,||\pmb{a}||=1 。
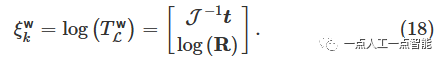
车辆的状态更新模型如下:
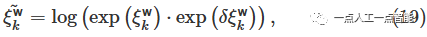
\delta \xi^{\text w}_k是通过连续迭代优化获得的姿态增量。
将点云转换为同一坐标系以估计里程计姿态。边缘特征\mathbf {p}_{\varepsilon k}^{\ell} \epsilon \mathbb{P} 转换为地面坐标系\tilde{\mathbf{p}}_{\varepsilon k}^{\text w} 。需要在地面坐标系中找到两个边缘点(\pmb {\text {p}}^{\pmb {\text {w}}}_{\pmb {\text {a}}},\pmb {\text {p}}^{\pmb {\text {w}}}_{\pmb {\text {b}}}) 。这两个点连接成一条直线,以构建点线残差。首先,在地面坐标系中搜索五个附近的边缘点。然后,根据等式(7)计算五个点的局部中心点。最后,使用\pmb {\text {p}}^{\pmb {\text {w}}}_{\pmb {\text {a}}} 选择中心前面的点,使用\pmb {\text {p}}^{\pmb {\text {w}}}_{\pmb {\text {b}}} 选择后面的点。从点到线的距离残差方程构造如下:
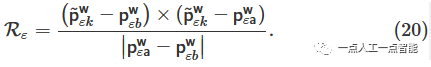
类似地,将平面特征点\mathbf {p}_{S k}^{\ell} \epsilon \mathbb{P} 转换为世界坐标系\mathbf {p}_{S k}^{\tilde{\text w}} 。在地面坐标系中搜索三个附近的平面点(\mathbf {p}_{S t}^{\text w},\mathbf {p}_{S u}^{\text w},\mathbf {p}_{S v}^{\text w}) 以形成平面。从点到平面的距离的残差方程如下:

我们将线残差和平面残差相结合,以获得姿态优化的损失函数,如下所示:
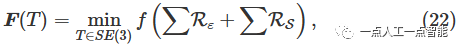
采用高斯-牛顿法求解非线性优化问题。进行一阶泰勒展开,求解增量如下f(x+\Delta x)\approx f(x)+\mathcal{J}(x)\Delta x 。增量方程式改写如下:

这里\mathcal{J} 是雅可比矩阵,\mathcal{H} 是定义为\mathcal{H}=\mathcal{J}(x)\mathcal{J}^T(x) 的Hessian矩阵,Δx是增量,g=-\mathcal{J}(x)f(x) 。将非线性问题转化为迭代解增量Δx。边缘残差的雅可比矩阵\mathcal{J}_{\varepsilon } 可通过以下公式计算:
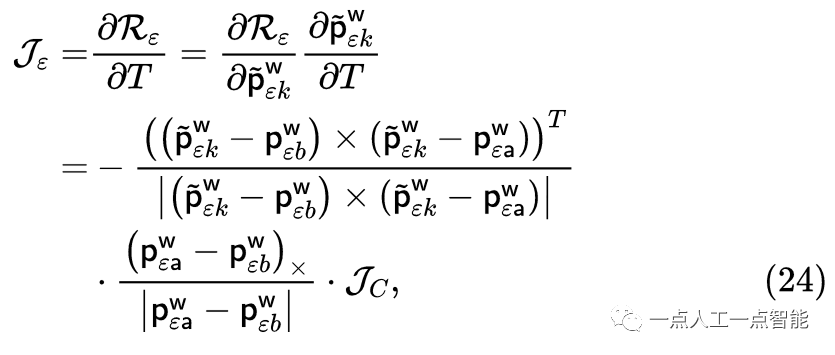
可以通过使用\delta \xi \epsilon \mathfrak{s e}(3) 的左扰动模型( left perturbation model)来估计雅可比矩阵\mathcal{J}_C :
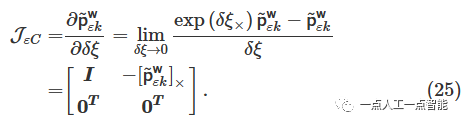
类似地,可以获得平面雅可比矩阵:
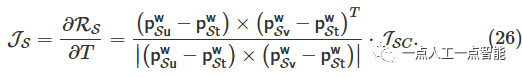
增量方程由雅可比矩阵求解,其中增量迭代优化,直到方程收敛。
随着时间推移,里程计不断产生累积误差,导致全局地图绘制不佳。累积误差可以通过环路检测和建图的全局优化来消除。为了加速地图优化,我们在回环检测和全局优化过程中采用了基于关键帧的方法。当两帧之间的姿态变化超过一定阈值时,选择当前帧作为关键帧。历史关键帧中省略了与当前帧类似的帧。两个相似帧的相对姿态作为约束边添加到图形优化中。我们使用两步循环检测方法。首先,使用快速高效的循环检测方法扫描前后信息[27]从历史关键帧中找到闭环候选帧。扫描前后信息引入了“旋转不变性”描述子,以快速检测不同方向上发生的循环。然后,使用ICP将当前帧与候选帧进行匹配,以获得两帧之间的分数。如图6所示,如果分数小于预设阈值,则在两帧中发生循环。循环的两个帧之间的相对位置作为约束边添加到图优化系统GTSAM[28]中。该优化系统可以有效地优化建图,消除累积误差。相应地更新历史位置和全局建图。
我们首先在KITTI里程计基准[15]上验证了所提出的系统中前端里程计的准确性和有效性。在测试中,仅使用了激光雷达的数据。数据集是从包括城市、农村和公路在内的大型复杂场景中收集的。选择提供地面真实值的序列00-10来评估算法。11个序列中有23201帧和22km的轨道长度。使用KITTI提供的里程计指标测试里程计的准确性。计算不同长度的平移和旋转误差,具体而言,每100m至800m计算一次。KITTI里程计基准定义的误差ARE和ATE的平均值分别表示平均旋转误差和平均平移误差。值越小表示算法的精度越好。
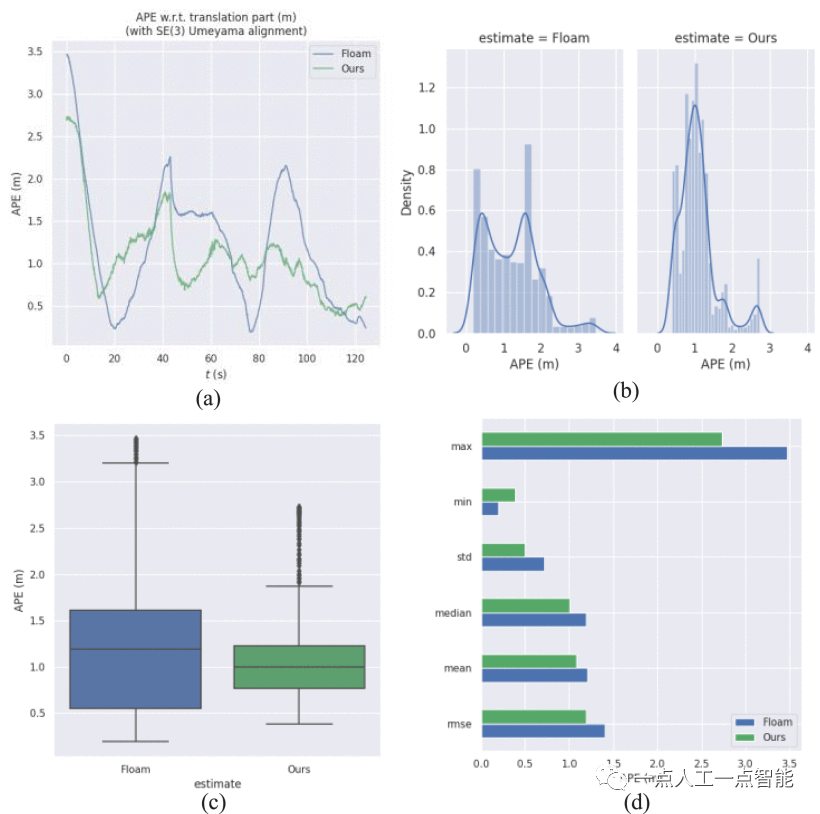
将所提出的里程测量方法(不使用环路检测)与最先进的轨迹算法FLOAM进行了比较。图7显示了我们的算法、FLOAM和地面真值在11个序列上的三种轨迹的比较。红色实线是我们算法的轨迹,蓝色实线是FLOAM里程表轨迹,绿色虚线是GPS/INS的地面真值。由于所提出的算法去除了一些冗余点。提取的特征点在六个自由度上更均匀地分布。因此,在大多数序列上,我们的算法比FLOAM更接近实际情况。所有轨迹基本上都与地面真值一致。图8显示了所提出的里程计估计的准确性,我们比较了FLOAM和所提出的算法之间由里程计估计的绝对姿态误差(APE)。所提出的算法的APE小于FLOAM,我们的算法更准确。误差波动范围较小,我们的系统更稳定。所提出的算法在包括均方根误差(RMSE)和标准差(STD)在内的其他评估指标上也小于FLOAM。实验证明,该算法能够在大规模城市环境中准确定位。

我们从KITTI里程计基准中选择了三个具有代表性的城市场景序列00、05和07进行分析。图9显示了SLAM系统在具有KITTI 00序列的大型城市环境中创建的建图结果,以及建图位置和方向的误差。所提出的算法能够处理移动对象的上述场景。该算法在x、y和偏航方向上的定位误差很小。如图9所示,x、y和偏航中的2D姿态分量接近地面,而高度(altitude)、横滚(roll)和俯仰(pitch)方向存在一些误差。这些误差可归因于激光雷达难以捕捉斜率和瞬时方向变化。在平坦的城市环境中,定位精度受影响较小。因此,所提出的SLAM系统在大规模城市环境中实现了精确定位。
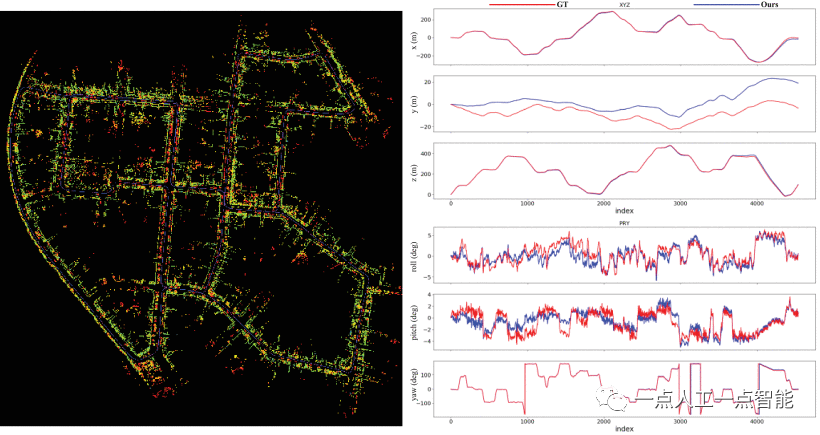
车辆的轨迹在KITTI 05序列中弯曲,长度为2223 m。车辆从不同方向通过同一十字路口,导致环路检测困难。由于引入了旋转不变量描述子,扫描前后信息可以有效地检测上述场景中的环路。如图10所示,所提出的系统可以在KITTI 05场景中构建与真实环境基本一致的3D点云图。x、y和偏航方向的定位精度接近地面实况。如图11所示,序列07是与序列05不同的另一种城市场景。车辆环绕市区,按顺序07返回原点。在这种情况下,所提出的系统精确定位并构建低漂移3D点云地图。测试结果表明,该系统可以在KITTI的三种不同城市场景中准确定位和建图。
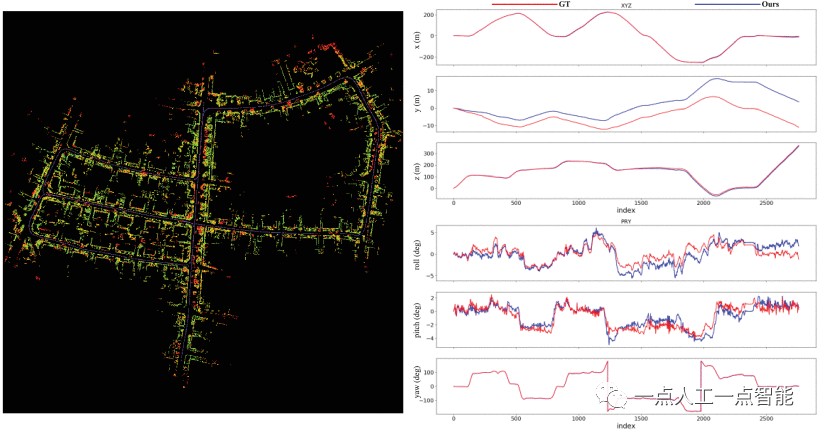
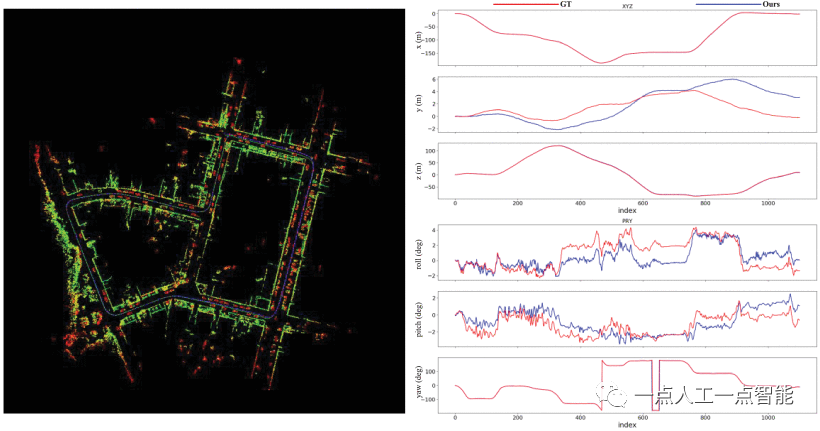
验证不同分辨率激光雷达特征提取算法的可行性。所提出的算法在MVSECD[16]数据集MVSECD上进行了测试,其中LiDAR的水平和垂直分辨率与KITTI的不同。如图12所示,蓝色实线是我们算法的轨迹,红线是地面真值。我们的系统在不同的城市场景中实现了卓越的定位精度。在第1天和第2天,所提出的系统获得的轨迹接近地面真实情况,这验证了使用深度信息而不依赖于激光雷达分辨率的特征点提取方法的有效性,以及所提出的SLAM系统在复杂城市环境中应用的鲁棒性。
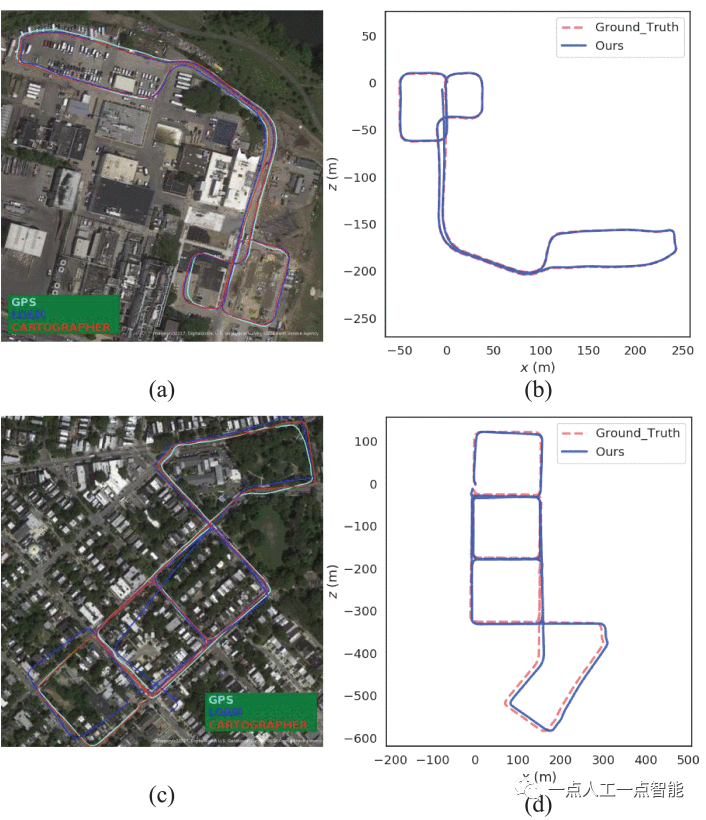
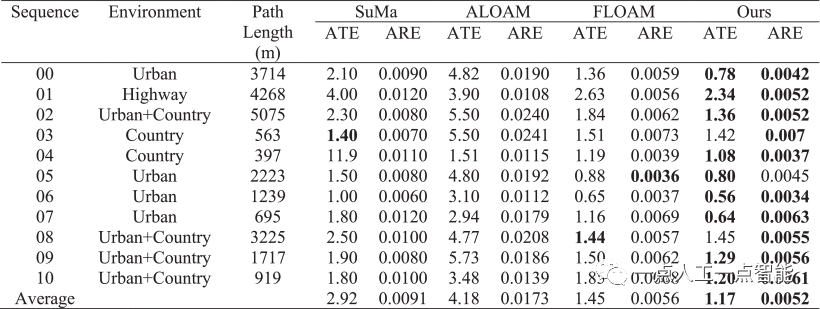
在KITTI序列00上测试了所提出的SLAM系统的实时性能。将系统的运行时间与ALOAM和FLOAM进行了比较。我们在带有Intel Core i7-10700 2.90GHz CPU的PC平台上进行了实验,测试环境基于ROS Melodic和Ubuntu 18.04 LTS。在前端,分别测试了地面分割、特征提取和距离姿态估计的运行时间。在后端,环路检测和姿态图优化被结合为一个模块来测试时间。如表2所示,行驶地面分割模块、特征提取模块和里程计位置估计模块的平均运行时间分别为26、29和21ms。整个前端平均花费76ms。与ALOAM和FLOAM相比,所提出的使用自适应选择方式的特征提取算法提取的点更少。因此,我们系统中的姿态估计花费更少的时间。我们系统中前端里程计的运行时间比ALOAM快23ms。所提出的系统中的前端和FLOAM花费的时间几乎相等。随着绘制过程中点云数量的增加,FLOAM和ALOAM的绘制时间也在增加。然而,我们的系统具有较少的特征点,因此实时建图更好。对于后端,环路在车辆运行一段时间后发生。只有在环路发生时,建图才会优化。我们使用2Hz的较低频率来检测环路。整个后端平均花费290毫秒。
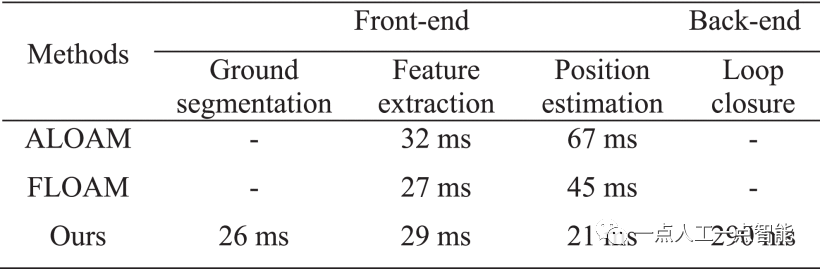
由于需要优化和更新全局地图和姿态,后端比前端花费更多的时间。需要注意的是,全局建图的优化和更新仅在环路发生时执行,而不是在每一帧时执行。因此,它对系统实时性能的影响可以忽略不计。测试结果表明,所提出的SLAM系统在所有上述测试中都取得了优异的实时性能。该系统可以应用于具有资源约束设备的自动驾驶车辆。
本文提出了一种轻量级实时3D激光雷达SLAM系统,以解决大型复杂城市环境中自动驾驶车辆的定位和建图问题。该系统包括地面分割、深度编码、基于改进PCA的特征提取和环路检测。
根据深度信息对无序的非地面点云进行编码。编码的点云保持三维信息而不投影到2D平面上。这种编码方法可以应用于具有不同分辨率的激光雷达。改进PCA中的邻域点自适应选择方法提高了特征提取的速度。通过根据距离选择不同数量的特征点,可以在六个自由度中提取均匀分布的点,以提高里程计的定位精度。
在KITTI数据集上,里程计的平均平移误差仅为1.17%,平均旋转误差仅为0.052(°/1m)。由于通过自适应特征提取方法提取的稀疏点,里程计中的姿态估计仅花费21ms。整个前端花费76ms,实现了实时性能。Scan Context和ICP用于回环检测,以消除建图累积误差。使用基于图的优化方法来优化全局建图。为了证明所提出的系统在不同城市场景中的鲁棒性,在KITTI和MVSECD数据集上评估了系统的性能。在上述两个数据集的不同场景中,系统的定位精度可以接近地面实况。